
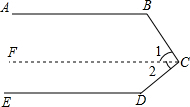
 填写适当的理由:如图,已知:AB∥ED,你能求出∠B+∠BCD+∠D的大小吗?
填写适当的理由:如图,已知:AB∥ED,你能求出∠B+∠BCD+∠D的大小吗?

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 填写适当的理由:如图,已知:AB∥ED,你能求出∠B+∠BCD+∠D的大小吗?
填写适当的理由:如图,已知:AB∥ED,你能求出∠B+∠BCD+∠D的大小吗?查看答案和解析>>
科目:初中数学 来源:初中几何同步单元练习册 第1册 题型:022
为下面简单推理填写适当的理由:
如图,
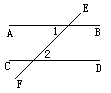
因为∠1=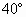 ,∠2=
,∠2=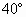 (已知),
(已知),
所以∠1=∠2( ),
所以AB∥CD( ).
查看答案和解析>>
科目:初中数学 来源:2016届河南南阳新野文府书院七年级上学期期末数学试卷(解析版) 题型:解答题
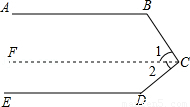
填写适当的理由:如图,已知:AB∥ED,你能求出∠B+∠BCD+∠D的大小吗?
解:过点C画FC∥AB
∵AB∥ED( )
FC∥AB( )
∴FC∥ED( )
∴∠B+∠1=180°
∠D+∠2=180°( )
∴∠B+∠1+∠D+∠2= °( )
即:∠B+∠BCD+∠D=360°.

查看答案和解析>>
科目:初中数学 来源:2016届河南南阳新野文府书院七年级上学期期末数学试卷(解析版) 题型:解答题
填写适当的理由:如图,已知:AB∥ED,你能求出∠B+∠BCD+∠D的大小吗?
解:过点C画FC∥AB
∵AB∥ED( )
FC∥AB( )
∴FC∥ED( )
∴∠B+∠1=180°
∠D+∠2=180°( )
∴∠B+∠1+∠D+∠2= °( )
即:∠B+∠BCD+∠D=360°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com