【题目】已知：sin(﹣x)=﹣sinx， cos(﹣x)=cosx，sin（x+y）=sinxcosy+cosxsiny，则下列各式不成立的是（ ）
A. cos（﹣45°）= 
B. sin75°= 
C. sin2x=2sinxcosx D. sin（x﹣y）=sinxcosy﹣cosxsiny
科目：初中数学 来源： 题型：
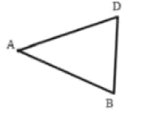
【题目】如图，点O是等边△ABC内一点，D是△ABC外的一点，∠AOB=110°，∠BOC=α，△BOC≌△ADC，∠OCD=60°，连接OD．
（1）求证：△OCD是等边三角形．
（2）当α=150°时，试判断△AOD的形状（按角分类），并说明理由．
（3）求∠OAD的度数．
（4）探究：当α= 时，△AOD是等腰三角形．（不必说明理由）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为响应珠海环保城市建设，我市某污水处理公司不断改进污水处理设备，新设备每小时处理污水量是原系统的1.5倍，原来处理1200m3污水所用的时间比现在多用10小时．
（1）原来每小时处理污水量是多少m2？
（2）若用新设备处理污水960m3，需要多长时间？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知:如图，三角形ABC中，D是BC边上一点.
(1)过点D作AB、AC的平行线分别交AB于点E,交AC于点F;
(2)说明:∠EDF=∠A;
(3)说明:∠A+∠B+∠C=180°.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某广告公司设计一幅周长为16米的矩形广告牌，广告设计费为每平方米2000元．设矩形一边长为x，面积为S平方米．
（1）求S与x之间的函数关系式，并写出自变量x的取值范围；
（2）设计费能达到24000元吗？为什么？
（3）当x是多少米时，设计费最多？最多是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明到某服装商场进行社会调查，了解到该商场为了激励营业员的工作积极性，实行“月总收入=基本工资+计件奖金”的方法，并获得如下信息：
营业员A：月销售件数200件，月总收入3400元；
营业员B：月销售件数300件，月总收入3700元；
假设营业员的月基本工资为x元，销售每件服装奖动y元．
(1)求x和y的值；
(2)商场为了多销售服装，对顾客推荐一种购买方式：如果购买甲服装3件，乙服装2件，丙服袋1件共需390元：如果购买甲服装1件，乙服装2件，丙服装3件共需370元．某顾客想购买甲、乙、丙服装各一件共需多少元?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠MON＝90°，正方形ABCD的顶点A、B分别在OM、ON上，AB＝13，OB＝5，E为AC上一点，且∠EBC＝∠CBN，直线DE与ON交于点F．
（1）求证BE＝DE；
（2）判断DF与ON的位置关系，并说明理由；
（3）△BEF的周长为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2019年5月26日振奋人心的“数博会”在我省贵阳市隆重召开。某校组织部分师生前往参观学习,租用A、B两种型号的旅游车共8辆。一辆A型车可坐40人,一辆B型车可坐35人。
(1)若前往参观的师生共310人,为了刚好将全部师生送达目的地,应分别租用A、B两种型号的旅游车各多少辆?
(2)若A型号的车每辆租金需220元,B型号的车每辆租金需160元,学校要求总租车费用不超过1540元,那么最多可租用多少辆A型号的旅游车?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是小欣设计的“利用等腰三角形做菱形”的尺规作图过程．
己知：等腰
求作：点
，使得四边形
为菱形．
做法：①作
的角平分线
，交线段
于点
；
②以点为圆心，长为半径圆弧，交的延长线于点；
③连接
，所以四边形为菱形，点即为所求．
根据小新设计的尺规作图过程．
（1）使用直尺和圆规补全图形；（保留作图痕迹）
（2）完成下面的证明．
证明：
平分，
（______________________________________）（填推理的依据）
∴四边形为平行四边形（______________________________________）（填推理的依据）
，
∴四边形为菱形（______________________________________）（填推理的依据）
（3）请你设计一种不同于小欣的，利用等腰
（其中
）作菱形的方法．
要求：写出简要思路，并尺规作图．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
