
分析 (1)是不确定事件,因为袋子中红球的个数不确定;
(2)用剩下的白球数量除以总数即可得到摸到白球的概率;
(3)设应该添加红球x个,白球y个,根据摸到红球的概率是摸到白球概率的$\frac{1}{4}$,列出算式,求出x,y之间的关系,再根据往袋子里再添加数量尽可能少的红球、白球,从而得出添加红球,白球的数量.
解答 解:(1)是不确定事件,理由如下:
∵袋子里有1个红球,第一次摸出一个球不放回,第二次从剩下的球中任意摸一个球,
∴两次摸到的小球有可能都是红球也有可能是白球,
∴红球的数量不确定,
∴摸到红球”这个事件是不确定事件;
(2)∵袋子里有1个红球,6个白球,第一次摸出一个白球不放回,再从剩下的球中摸出一个,
∴摸到白球的概率是=$\frac{6-1}{6+1-1}$=$\frac{5}{6}$;
(3)设应该添加红球x个,白球y个,根据题意得:
$\frac{1+x}{x+1+6+y}$=$\frac{y+6}{x+1+6+y}$×$\frac{1}{4}$,
解得:4x-y=2,
∵往袋子里再添加数量尽可能少的红球、白球,
∴x=1,y=2,
∴应该添加红球1个,白球2个.
点评 本题主要考查了概率公式,解题的关键是根据概率公式只需求出各自所占的比例大小即可,求比例时,应注意记清各自的数目,难度适中.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:选择题
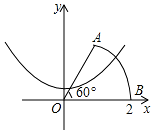 如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )| A. | -4<k<$\frac{3}{4}$ | B. | -2<k<$\frac{3}{4}$ | C. | -4<k<$\sqrt{3}$-1 | D. | -2<k<$\sqrt{3}$+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
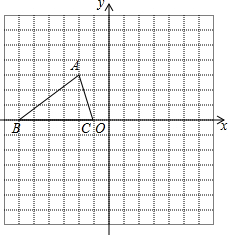 如图,已知△ABC的三个顶点坐标为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点坐标为A(-2,3)、B(-6,0)、C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点D,E在AB,AC上,连接DE,DF平分∠BDE交BC于点F,∠BDF+∠DFC=180°,∠AED=∠BFD.
如图,点D,E在AB,AC上,连接DE,DF平分∠BDE交BC于点F,∠BDF+∠DFC=180°,∠AED=∠BFD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
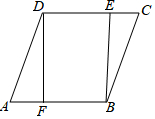 如图,已知四边形ABCD是菱形,DF⊥AB于点F,BE⊥CD于点E.
如图,已知四边形ABCD是菱形,DF⊥AB于点F,BE⊥CD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com