
| ��ȡ��ƹ������n | 200 | 500 | 1000 | 1500 | 2000 |
| �ŵ�ƷƵ��m | 188 | 471 | 946 | 1426 | 1898 |
| �ŵ�ƷƵ��$\frac{m}{n}$ | 0.940 | 0.942 | 0.946 | 0.951 | 0.949 |
���� ��1������ͳ�Ʊ��е����ݣ���������㣬Ȼ���������ἴ�ɣ�
��2������Ƶ�ʹ��Ƹ��ʣ�Ƶ�ʶ���0.946���Ҳ��������Կ��Թ�������ƹ�����ŵ�Ʒ�����ʵĹ���ֵ��0.946��
��3�����û���ĸ�����������ܸ������ɣ�
����Ӵ���ȡ����x�������ݽ�����Ⱥ�ʹ�Ӵ�������һ���ǻ���ĸ��ʲ�С��$\frac{1}{3}$���г�����ʽ���ⲻ��ʽ���ɣ�
��� 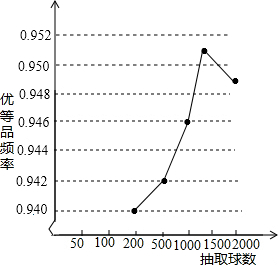 �⣺��1����ͼ��
�⣺��1����ͼ��
��2������ƹ�����ŵ�Ʒ�����ʵĹ���ֵ��0.946��
��3���١ߴ���һ������5+13+22=40����������5������
��Ӵ�������һ�����ǻ���ĸ���Ϊ��$\frac{5}{40}$=$\frac{1}{8}$��
����Ӵ���ȡ����x�������������
$\frac{5+x}{40}$��$\frac{1}{3}$�����x��8$\frac{1}{3}$��
������ȡ����9������
���� ���⿼��������Ƶ�ʹ��Ƹ��ʣ������ظ�ʵ��ʱ���¼�������Ƶ����ij���̶�λ�����Ұڶ������Ұڶ��ķ���Խ��ԽС���������Ƶ���ȶ��Զ�����������Ƶ�ʵļ������������Ƹ��ʣ�����̶��Ľ���ֵ��������¼��ĸ��ʣ���Ƶ�ʹ��Ƹ��ʵõ����ǽ���ֵ����ʵ����������ֵ࣬Խ��Խ��ȷ��Ҳ������Ƶ�ʷֲ�����ͼ�Լ����ʹ�ʽ������=������������������֮�ȣ�


 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | |-2|��2 | B�� | -2��$\root{3}{-8}$ | C�� | -2��$-\frac{1}{2}$ | D�� | -2��$\sqrt{{{��-2��}^2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��4��5 | B�� | 5��12��13 | C�� | 6��8��10 | D�� | 2��3��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com