
科目:初中数学 来源: 题型:解答题
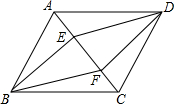 如图,在□ABCD中,E、F是对角线AC上的两点,AE=CF.
如图,在□ABCD中,E、F是对角线AC上的两点,AE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
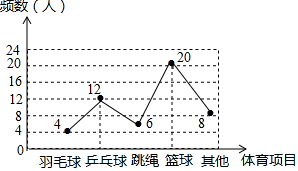 体育老师对八年级(2)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成如图所示的折线统计图.由图可知,最喜欢篮球的学生的频率是( )
体育老师对八年级(2)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成如图所示的折线统计图.由图可知,最喜欢篮球的学生的频率是( )| A. | 16% | B. | 24% | C. | 30% | D. | 40% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com