
 求证:两条平行直线被第三条直线所截,一对同旁内角的平分线互相垂直
求证:两条平行直线被第三条直线所截,一对同旁内角的平分线互相垂直分析 两条平行直线被第三条直线所截,一对同旁内角的和是180°,然后根据角平分线的性质求出这对同旁内角和的一半是90°,即可求证一对同旁内角的平分线互相垂直.
解答  证明:∵AB∥CD(已知)
证明:∵AB∥CD(已知)
∴∠BOM+∠OMD=180°( 两直线平行,同旁内角互补).
∵MN,OP分别平分∠OMD,∠BOM(已知),
∴2∠POM+2∠NMO=180°(角平分线的定义)
∴∠POM+∠PMO=90°(等式的性质)
∴∠MGO=90°(三角形的内角和定理)
∴MN⊥OP.
故答案为:180°,两直线平行,同旁内角互补,180°,∠POM+∠PMO,∠MGO=90°
点评 本题主要考查了平行线的性质以及三角形内角和定理的运用,利用平行线的性质以及角平分线的性质,求证两直线相交所得的夹角是90°是解决问题的关键.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个数的绝对值一定是正数 | |
| B. | 一个数的相反数的绝对值一定是正数 | |
| C. | 一个数的绝对值的相反数一定是负数 | |
| D. | 一个数的绝对值一定是非负数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
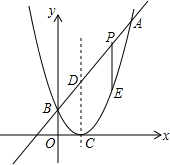 如图,己知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,与对称轴交于D(m,2),其中B点在y轴上
如图,己知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,与对称轴交于D(m,2),其中B点在y轴上查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com