
 已知:如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
已知:如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.分析 (1)由AB与CD平行,利用两直线平行内错角相等得到一对角相等,再由已知角相等,等量代换得到一对同位角相等,利用同位角相等两直线平行即可得证;
(2)由EF与OC平行,利用两直线平行同旁内角互补得到∠BFE+∠DOC=180°,结合已知即可求得结果.
解答 (1)证明:∵AB∥CD,
∴∠A=∠C ( 两直线平行,内错角相等 ),
又∵∠1=∠A,
∴∠C=∠1,
∴FE∥OC,(同位角相等,两直线平行)
(2)解:∵FE∥OC,
∴∠BFE+∠DOC=180°( 两直线平行,同旁内角互补 ),
又∵∠BFE=70°,
∴∠DOC=110°.
点评 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 我国古代的数学家很早就发现并应用勾股定理,而且尝试对勾股定理做出证明.最早对勾股定理进行证明的是三国时期吴国的数学家赵爽.如图,就是著名的“赵爽弦图”.△ABE,△BCF,△CDG和△DAH是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.已知AB=5,AH=3,求EF的长.小敏的思路是设EF=x,根据题意,小敏所列的方程是32+(x+3)2=52.
我国古代的数学家很早就发现并应用勾股定理,而且尝试对勾股定理做出证明.最早对勾股定理进行证明的是三国时期吴国的数学家赵爽.如图,就是著名的“赵爽弦图”.△ABE,△BCF,△CDG和△DAH是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.已知AB=5,AH=3,求EF的长.小敏的思路是设EF=x,根据题意,小敏所列的方程是32+(x+3)2=52.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
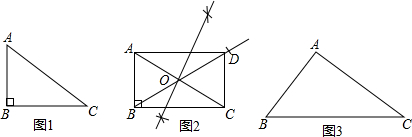
 如图,在△ABC中,∠C=90°,∠A=30°,BC=5,在△DEF中,∠EDF=90°,∠DEF=45°,DE=3.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动,在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动到点F与点B重合为止),连接BE,设AD=x,BE=y.下列结论:①当x=2时,y=$\sqrt{73}$;②当x=10-4$\sqrt{3}$时,BE∥AC;③当x=7-3$\sqrt{2}$时,∠EBD=22.5°,其中正确有( )
如图,在△ABC中,∠C=90°,∠A=30°,BC=5,在△DEF中,∠EDF=90°,∠DEF=45°,DE=3.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动,在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动到点F与点B重合为止),连接BE,设AD=x,BE=y.下列结论:①当x=2时,y=$\sqrt{73}$;②当x=10-4$\sqrt{3}$时,BE∥AC;③当x=7-3$\sqrt{2}$时,∠EBD=22.5°,其中正确有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
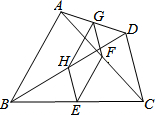 如图,在四边形ABCD中,E,F,G,H分别是BC,AC,AD,BD的中点,要使四边形EFGH是菱形,四边形ABCD的边AB、CD应满足的条件是AB=CD.
如图,在四边形ABCD中,E,F,G,H分别是BC,AC,AD,BD的中点,要使四边形EFGH是菱形,四边形ABCD的边AB、CD应满足的条件是AB=CD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )| A. | (3,4)或(2,4) | B. | (2,4)或(8,4) | C. | (3,4)或(8,4) | D. | (3,4)或(2,4)或(8,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com