

 习题精选系列答案
习题精选系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
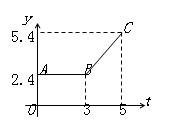
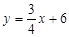 与x轴、y轴分别交于A、B两点,C为OA中点;
与x轴、y轴分别交于A、B两点,C为OA中点;
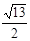 个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t( ),求y于t的函数关系式;
个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t( ),求y于t的函数关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
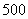 只同一型号的零件,他们生产的零件
只同一型号的零件,他们生产的零件 (只)与生产时间
(只)与生产时间 (分)的函数关系的图象如图所示。根据图象提供的信息解答下列问题:
(分)的函数关系的图象如图所示。根据图象提供的信息解答下列问题:
 倍,请分别求出甲、乙两人生产全过程中,生产的零件
倍,请分别求出甲、乙两人生产全过程中,生产的零件 (只)与生产时间
(只)与生产时间 (分)的函数关系式;
(分)的函数关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
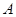 种果汁原料和
种果汁原料和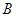 种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制
种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制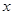 千克,两种饮料的成本总额为
千克,两种饮料的成本总额为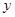 元.
元.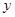 与
与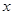 之间的函数关系式;
之间的函数关系式;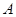 种果汁原料和17.2千克
种果汁原料和17.2千克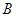 种果汁原料试制甲、乙两种新型饮料,右表是试验的相关数据;请你列出关于
种果汁原料试制甲、乙两种新型饮料,右表是试验的相关数据;请你列出关于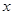 且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使
且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使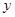 值最小,最小值是多少?
值最小,最小值是多少?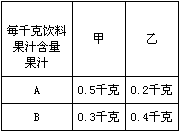
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com