
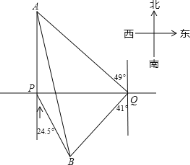
【题目】一轮船在![]() 处测得灯塔
处测得灯塔![]() 在正北方向,灯塔
在正北方向,灯塔![]() 在南偏东
在南偏东![]() 方向,轮船向正东航行了
方向,轮船向正东航行了![]() ,到达
,到达![]() 处,测得
处,测得![]() 位于北偏西
位于北偏西![]() 方向,
方向,![]() 位于南偏西
位于南偏西![]() 方向.
方向.
(1)线段![]() 与
与![]() 是否相等?请说明理由;
是否相等?请说明理由;
(2)求![]() 、
、![]() 间的距离(参考数据
间的距离(参考数据![]() ).
).
【答案】(1)BQ=PQ,理由见解析;(2)4000m
【解析】
(1)首先由已知求出∠PBQ和∠BPQ的度数进行比较得出线段BQ与PQ是否相等;
(2)先由已知求出∠PQA,再由直角三角形PQA求出AQ,由(1)得出BQ=PQ=2400m,又由已知得∠AQB=90°,所以根据勾股定理求出A,B间的距离.
解:(1)线段BQ与PQ相等.
∵∠PQB=90°-41°=49°,
∠BPQ=90°-24.5°=65.5°,
∴∠PBQ=180°-49°-65.5°=65.5°,
∴∠BPQ=∠PBQ,
∴BQ=PQ;
(2)∵∠AQB=180°-49°-41°=90°,
∠PQA=90°-49°=41°,
∴AQ=![]() =
=![]() ==3200,
==3200,
BQ=PQ=2400,
∴AB2=AQ2+BQ2=32002+24002,
∴AB=4000,
答:A、B的距离为4000m


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
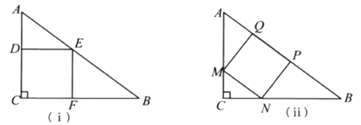
【题目】一块直角三角形的木板,它的一条直角边AC长为1.5米,面积为1.5平方米.现在要把它加工成一个正方形桌面,甲、乙两人的加工方法分别如图(ⅰ)、(ⅱ)所示,记两个正方形面积分别为S1、S2,请通过计算比较S1与S2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
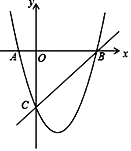
【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商人将进货单价为![]() 元的某种商品按
元的某种商品按![]() 元销售时,每天可卖出
元销售时,每天可卖出![]() 件.现在他采用提高售价的办法增加利润,已知这种商品销售单价每涨
件.现在他采用提高售价的办法增加利润,已知这种商品销售单价每涨![]() 元,销售量就减少
元,销售量就减少![]() 件,那么他将售价每个定为________元时,才能使每天所赚的利润最大,每天最大利润是________元.
件,那么他将售价每个定为________元时,才能使每天所赚的利润最大,每天最大利润是________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
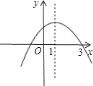
【题目】已知二次函数![]() 的图象如图所示,则关于
的图象如图所示,则关于![]() 的一元二次方程
的一元二次方程![]() 的根为________;不等式
的根为________;不等式![]() 的解集是________;当
的解集是________;当![]() ________时,
________时,![]() 随
随![]() 的增大而减小.
的增大而减小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在![]() 中,
中,![]() 是高,
是高,![]() 是角平分线,它们相交于点
是角平分线,它们相交于点![]() ,
,![]() .求
.求![]() 和
和![]() 的度数.
的度数.
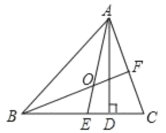
(2)一个多边形的内角和是外角和的3倍,它是几边形?若这个多边形的各个内角都相等,求这个多边形的每个内角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则tan∠FBC的值为( )
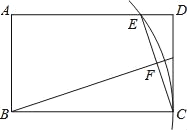
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com