
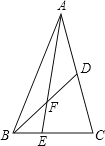
【题目】如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF﹣S△BEF= .
【答案】2;
【解析】
试题分析:S△ADF﹣S△BEF=S△ABD﹣S△ABE,所以求出三角形ABD的面积和三角形ABE的面积即可,因为EC=2BE,点D是AC的中点,且S△ABC=12,就可以求出三角形ABD的面积和三角形ABE的面积.
解:∵点D是AC的中点,
∴AD=![]() AC,
AC,
∵S△ABC=12,
∴S△ABD=![]() S△ABC=
S△ABC=![]() ×12=6.
×12=6.
∵EC=2BE,S△ABC=12,
∴S△ABE=![]() S△ABC=
S△ABC=![]() ×12=4,
×12=4,
∵S△ABD﹣S△ABE=(S△ADF+S△ABF)﹣(S△ABF+S△BEF)=S△ADF﹣S△BEF,
即S△ADF﹣S△BEF=S△ABD﹣S△ABE=6﹣4=2.
故答案为:2.


科目:初中数学 来源: 题型:
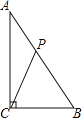
【题目】如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )
A.5 B.5或8 C.![]() D.4或
D.4或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
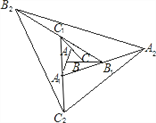
【题目】如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2010,最少经过几次操作 ( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,∠COD=90°,直线AB与OC交于点B,与OD交于点A,射线OE和射线AF交于点G.
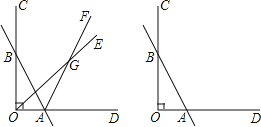
(1)若OE平分∠BOA,AF平分∠BAD,∠OBA=30°,则∠OGA=
(2)若∠GOA=![]() ∠BOA,∠GAD=
∠BOA,∠GAD=![]() ∠BAD,∠OBA=30°,则∠OGA=
∠BAD,∠OBA=30°,则∠OGA=
(3)将(2)中“∠OBA=30°”改为“∠OBA=α”,其余条件不变,则∠OGA= (用含α的代数式表示)
(4)若OE将∠BOA分成1:2两部分,AF平分∠BAD,∠ABO=α(30°<α<90°),求∠OGA的度数(用含α的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】试解答下列问题:
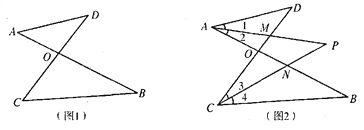
(1)在图1我们称之为“8字形”,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)仔细观察,在图2中“8字形”的个数是 个;
(3) 在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试写出∠B与∠P、∠D之间数量关系 .
查看答案和解析>>
科目:初中数学 来源: 题型:
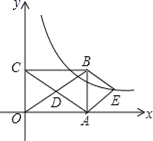
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小洪根据演讲比赛中九位评委所给的分数制作了如下表格:
平均数 | 中位数 | 众数 | 方差 |
8.5 | 8.3 | 8.1 | 0.15 |
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( ).
A.平均数 B.中位数 C.众数 D.方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com