
【题目】已知:数轴上点A、B、C表示的数分别为a、b、c,点O为原点,且a、b、c满足(a﹣6)2+|b﹣2|+|c﹣1|=0.
(1)直接写出a、b、c的值;
(2)如图1,若点M从点A出发以每秒1个单位的速度向右运动,点N从点B出发以每秒3个单位的速度向右运动,点R从点C出发以每秒2个单位的速度向右运动,点M、N、R同时出发,设运动的时间为t秒,t为何值时,点N到点M、R的距离相等;
(3)如图2,若点P从点A出发以每秒1个单位的速度向左运动,点Q从点B出发以每秒3个单位的速度向左运动,点P,Q同时出发开始运动,点K为数轴上的一个动点,且点C始终为线段PK的中点,设运动时间为t秒,若点K到线段PC的中点D的距离为3时,求t的值.
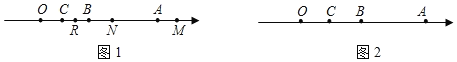
【答案】(1)a=6,b=2,c=1;(2)t为1s时,点N到点M、R的距离相等;(3)t=3或7.
【解析】
(1)根据非负数的性质,列出方程进行解答便可;
(2)先用t的代数式表示NM、NR,再由NM=NR列出t的方程便可;
(3)用t的代数式表示P点,再根据中点公式用t表示D点和K点,再由两点距离公式由DK=3列出t的方程进行解答便可.
(1)∵(a﹣6)2+|b﹣2|+|c﹣1|=0,
∴a﹣6=0,b﹣2=0,c﹣1=0,
∴a=6,b=2,c=1;
(2)由题意得:(6+t)﹣(2+3t)=(2+3t)﹣(1+2t),
解得:t=1,
∴t为1s时,点N到点M、R的距离相等;
(3)由题意知,P点表示的数为:6﹣t.
∵D是PC的中点,
∴D表示的数为:![]() ,
,
∵C是PK的中点,
∴点K表示的数为:2×1﹣(6﹣t)=t﹣4.
∵KD=3,
∴|(t﹣4)![]() |=3,
|=3,
∴t=3或7.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在直角梯形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,且M在AD上以1cm/s的速度由A向D运动,点N在BC上以2cm/s的速度由C向B运动.
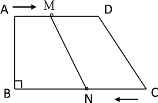
(1)几秒后MNCD为平行四边形?
(2)几秒后ABNM为矩形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上的A、B两点所对应的数分别为a、b.P为数轴上的一个动点.其中a,b满足(a﹣1)2+|b+5|=0,
(1)若点P为AB的中点,求P点对应的数.
(2)若点P从A点出发,以每秒2个单位的速度向左运动,t秒后,求P点所对应的数以及PB的距离.
(3)若数轴上点M、N所对应的数为m、n,其中A为PM的中点,B为PN的中点,无论点P在何处,![]() 是否为一个定值?若是,求出定值:若不是,请说明理由.
是否为一个定值?若是,求出定值:若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2-4=0.
(1)当m为何值时,方程有两个不相等的实数根?
(2)若边长为5的菱形的两条对角线的长分别为方程两根的2倍,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
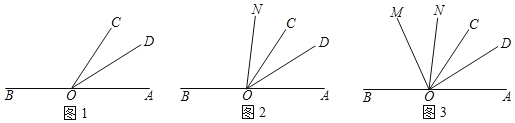
【题目】已知:点O为直线AB上一点,过点O作射线OC,使∠AOC=70°.
(1)如图1,若OD平分∠AOC,求∠DOB的度数;
(2)射线OM从OA出发,绕点O以每秒6°的速度逆时针旋转,同时,射线ON从OC出发绕点O以每秒4°的速度逆时针旋转,OM与ON同时出发(当ON首次与OB重合时,两条射线都停止运动),设运动的时间为t秒.
(i)如图2,在整个运动过程中,当∠BON=2∠COM时,求t的值;
(ⅱ)如图3,OP平分∠AOM,OQ平分∠BON,是否存在合适的t,使OC平分∠POQ,若存在,求出t的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
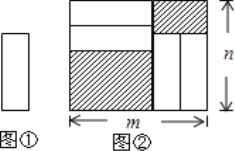
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
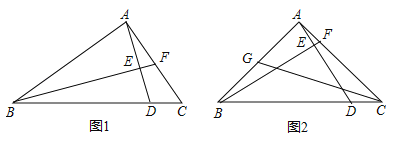
【题目】如图,直角△ABC中,∠BAC=90°,D在BC上,连接AD,作BF⊥AD分别交AD于E,AC于F.
(1)如图1,若BD=BA,求证:△ABE≌△DBE;
(2)如图2,若BD=4DC,取AB的中点G,连接CG交AD于M,求证:①GM=2MC;②AG2=AFAC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com