
 已知:如图,正方形ABCD的边长为6,BM,DN分别平分正方形的两个外角,且满足∠MAN=45°,连接MC,NC,MN.
已知:如图,正方形ABCD的边长为6,BM,DN分别平分正方形的两个外角,且满足∠MAN=45°,连接MC,NC,MN. 分析 (1)只要证明△ADN∽△MBA得$\frac{AD}{BM}$=$\frac{DN}{AB}$即可证明.
(2)先证明△CBM∽△NDC可以推出∠DCN+∠BCM=135°,由此即可解决问题.
解答 (1)证明: ∵BM,DN分别平分正方形的两个外角,
∵BM,DN分别平分正方形的两个外角,
∴∠CDN=∠CBM=45°,
∵四边形ABCD是正方形,
∴AD=AB=BC=CD,∠ADC=∠DCB=∠CBA=∠BAD=90°,
∴∠ADN=∠ABN=135°,
∵∠NAM=45°,
∠BAM+∠DAN=45°,∵∠BAM+∠AMB=45°,
∴∠DAN=∠AMB,
∴△ADN∽△MBA,
∴$\frac{AD}{BM}$=$\frac{DN}{AB}$,
∴BM•DN=AB•AD=36.
(2)∵BM•DN=BC•DC,
∴$\frac{BC}{DN}$=$\frac{BM}{DC}$,∵∠CBM=∠CDN,
∴△CBM∽△NDC,
∴∠DCN=∠BMC,
∵∠BCM+∠BMC=135°,
∴∠BCM+∠DCN=135°,
∴∠MCN=360°-∠BCD-∠BCM-∠DCN=135°.
点评 本题考查相似三角形的判定和性质、正方形的性质等知识,解题的关键是正确寻找相似三角形,利用相似三角形的性质解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
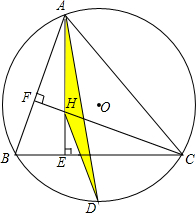 已知,△ABC内接于⊙O,∠BAC=60°,AE⊥BC,CF⊥AB.AE,CF相交于点H,点D为弧BC的中点,连接HD,AD.求证:△AHD为等腰三角形.
已知,△ABC内接于⊙O,∠BAC=60°,AE⊥BC,CF⊥AB.AE,CF相交于点H,点D为弧BC的中点,连接HD,AD.求证:△AHD为等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
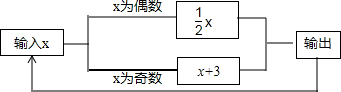
| A. | 6 | B. | 3 | C. | $\frac{3}{{2}^{2008}}$ | D. | 6027 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
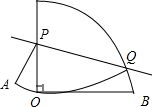 如图,是一个圆心角为90°的扇形,AO=2cm,点P在半径AO上运动,点Q在弧AB上运动,沿PQ将它以上的部分向下翻折,使翻折后的弧恰好过点O,则OP的最大距离为$\frac{2\sqrt{3}}{3}$.
如图,是一个圆心角为90°的扇形,AO=2cm,点P在半径AO上运动,点Q在弧AB上运动,沿PQ将它以上的部分向下翻折,使翻折后的弧恰好过点O,则OP的最大距离为$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com