
 一辆自行车在公路上行驶,中途发生了故障,停下修理一段时间后继续前进.已知行驶路程S(千米)与所用时间t(时)的函数关系的图象如图所示,那么自行车发生故障后继续前进的速度为( )
一辆自行车在公路上行驶,中途发生了故障,停下修理一段时间后继续前进.已知行驶路程S(千米)与所用时间t(时)的函数关系的图象如图所示,那么自行车发生故障后继续前进的速度为( )| A. | 20千米/时 | B. | $\frac{35}{3}$千米/时 | C. | 10千米/时 | D. | $\frac{50}{3}$千米/时 |
科目:初中数学 来源: 题型:填空题
 五子棋是一种两人对弈的棋类游戏,规则是:在正方形棋盘中,由黑方先行,白方后行,轮流弈子,下在棋盘横线与竖线的交叉点上,直到某一方首先在任一方向(横向、竖向或者是斜着的方向)上连成五子者为胜.如图,这一部分棋盘是两个五子棋爱好者的对弈图.观察棋盘,以点O为原点,在棋盘上建立平面直角坐标系,将每个棋子看成一个点,若黑子A的坐标为(7,5),则白子B的坐标为(5,1);为了不让白方获胜,此时黑方应该下在坐标为(3,7)或(7,3)的位置处.
五子棋是一种两人对弈的棋类游戏,规则是:在正方形棋盘中,由黑方先行,白方后行,轮流弈子,下在棋盘横线与竖线的交叉点上,直到某一方首先在任一方向(横向、竖向或者是斜着的方向)上连成五子者为胜.如图,这一部分棋盘是两个五子棋爱好者的对弈图.观察棋盘,以点O为原点,在棋盘上建立平面直角坐标系,将每个棋子看成一个点,若黑子A的坐标为(7,5),则白子B的坐标为(5,1);为了不让白方获胜,此时黑方应该下在坐标为(3,7)或(7,3)的位置处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 次数 | 第一次 | 第二次 | 第三次 | 第四次 |
| 甲 | 9.7 | 10 | 10 | 8.4 |
| 乙 | 9.2 | 10 | 9.7 | 9.2 |
| A. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,S甲2>S乙2 | B. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,$S_甲^2<S_乙^2$ | ||
| C. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,$S_甲^2>S_乙^2$ | D. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,$S_甲^2<S_乙^2$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
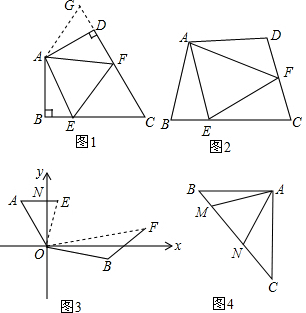
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com