
【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②DE长度的最小值为4;③四边形CDFE的面积保持不变;④△CDE面积的最大值为8.其中正确的结论是( )
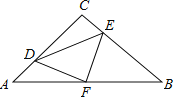
A.①②③B.①③C.①③④D.②③④
【答案】C
【解析】
①连接CF,构造全等三角形,证明△ADF≌△CEF即可.
②通过①可得△DFE是等腰直角三角形,则斜边DE=![]() DF,求得DF的最小值即可得到DE的最小值.
DF,求得DF的最小值即可得到DE的最小值.
③通过证明△ADF≌△CEF,进行等面积代换即可得出.
④通过结论③,换角度将四边形CDFE的面积分为△CDE与△DEF,令△DEF的面积最小即可.
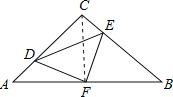
①连接CF.
∵△ABC为等腰直角三角形,
∴∠FCB=∠A=45°,CF=AF=FB,
∵AD=CE,
∴△ADF≌△CEF,
∴EF=DF,∠CFE=∠AFD,
∵∠AFD+∠CFD=90°
∴∠CFE+∠CFD=∠EFD=90°,
∴△EDF是等腰直角三角形,
故本选项正确;
②∵△DEF是等腰直角三角形,
∴当DE最小时,DF也最小,
即当DF⊥AC时,DE最小,此时DF=![]() BC=4,
BC=4,
∴DE=![]() DF=
DF=![]() ,
,
故本选项错误;
③∵△ADF≌△CEF,
∴S△CEF=S△ADF,
∴S四边形CDFE=S△DCF+S△CEF=S△DCF+S△ADF=S△ACF=![]() S△ABC
S△ABC
故本选项正确;
④当△CED面积最大时,由③知,此时△DEF的面积最小,此时,
S△CED=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=16﹣8=8,
故本选项正确;
综上所述正确的有①③④.
故选:C.


科目:初中数学 来源: 题型:
【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | | 8 | 0.4 |
乙 | | 9 | | 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (a≠0)图象如图所示,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>
(a≠0)图象如图所示,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>![]() ;④a-b+c>0;⑤若
;④a-b+c>0;⑤若![]() , 且
, 且![]() , 则
, 则![]() .其中正确的有( ).
.其中正确的有( ).
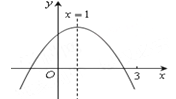
A. ①②③ B. ②④ C. ②⑤ D. ②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片![]() 纸沿对角线折叠,设重叠部分为△
纸沿对角线折叠,设重叠部分为△![]() ,那么,下列说法错误的是( )
,那么,下列说法错误的是( )
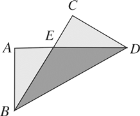
A.△![]() 是等腰三角形,
是等腰三角形,![]()
B.折叠后∠ABE和∠CBD一定相等
C.折叠后得到的图形是轴对称图形
D.△EBA和△EDC一定是全等三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF.
(1)求证:BE=BF;
(2)若∠ABE=20°,求∠BFE的度数;
(3)若AB=6,AD=8,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x=1是一元二次方程(m+1)x-mx+2m+3=0的一个根。
(1)求m的值,并写出此时的一元二次方程的一般形式
(2)把方程两根分别记为![]() ,
,![]() ,不解方程,求
,不解方程,求![]() +
+![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华商场为迎接家电下乡活动销售某种冰箱,每台进价为2500元,市场调研表明;当销售价定为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台,商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com