①证明:△=b
2-4ac=[-2(a+b)]
2-4×1×c
2=4[(a+b)
2-c
2],
∵a+b>c(三角形任意两边之和大于第三边),
∴△>0,
∴抛物线与x轴必有两个交点;
②证明:抛物线对称轴为直线x=-

=-
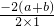
=2a,
解得a=b,
∴△ABC为等腰三角形,
直线与抛物线解析式联立得,
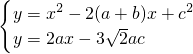
,
即x
2-2(a+b)x+c
2=2ax-3

ac,
整理得,x
2-6ax+c
2+3

ac=0,
∵△MNE与△MNF面积之比为2:1,
∴点E到MN的距离等于点F到MN的距离的2倍,
即点E的横坐标是点F的横坐标的2倍,
设点F的横坐标是x,则点E的横坐标是2x,
∴x+2x=6a,
解得x=2a,2x=4a,
∴x•2x=2a•4a=c
2+3

ac,
整理得c
2+3

ac-8a
2=0,
解得c=

a,c=-4

a(舍去),
∴a
2+b
2=2a
2=c
2,
∴△ABC为直角三角形,
故△ABC为等腰直角三角形;
③解:存在.
理由如下:S
△ABC=

×a×b=

×a×a=2,
∴a=b=2,
∴c=

a=2

,
∴抛物线解析式为y=x
2-2(a+b)x+c
2=x
2-8x+8,
∴PQ=

=
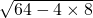
=4

,
∵圆与y轴相切,
∴半径r=2a=2×2=4,
∴弦心距=

=2

,
∴存在过P、Q两点,且与y轴相切的圆,圆心(4,2

)或(4,-2

).
分析:①列式求出根的判别式,再根据三角形的任意两边之和大于第三边判断出△>0,即可判断与x轴有两个交点;
②先根据抛物线对称轴公式求出a=b,再根据△MNE与△MNF面积之比为2:1,可以求出点E的横坐标是点F的横坐标的2倍,直线与抛物线解析式联立得到关于x的方程,即方程的一个解是另一个解的2倍,从而求出方程的两个根,再根据根与系数的关系中的两根之积列式求出a与c的关系,然后根据勾股定理逆定理即可证明;
③根据三角形的面积求出a、b的长度,然后求出c的长度,从而得到抛物线解析式,然后求出PQ的长度,再根据圆与y轴相切求出圆的半径,然后根据圆的半径、弦的一半,利用勾股定理求出弦心距即可得到圆心的坐标.
点评:本题是二次函数综合题,考查了利用根的判别式求抛物线与x轴的交点个数,联立直线与抛物线解析式求函数图象的交点坐标之间的关系,函数图象上两点间的距离的求解,半径、弦心距、半弦长组成的三角形的计算,综合性较强,对同学们能力要求较高,仔细分析,认真计算也不难求解.

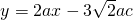 与抛物线交于E、F,与y轴交于点M,抛物线与y轴交于点N,若抛物线对称轴为直线x=2a,△MNE与△MNF面积之比为2:1,求证:△ABC为等腰直角三角形;
与抛物线交于E、F,与y轴交于点M,抛物线与y轴交于点N,若抛物线对称轴为直线x=2a,△MNE与△MNF面积之比为2:1,求证:△ABC为等腰直角三角形;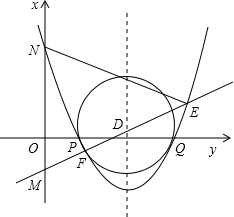
 =-
=-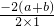 =2a,
=2a,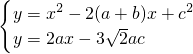 ,
, ac,
ac, ac=0,
ac=0, ac,
ac, ac-8a2=0,
ac-8a2=0, a,c=-4
a,c=-4 a(舍去),
a(舍去), ×a×b=
×a×b= ×a×a=2,
×a×a=2, a=2
a=2 ,
, =
=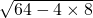 =4
=4 ,
, =2
=2 ,
, )或(4,-2
)或(4,-2 ).
).

 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.