
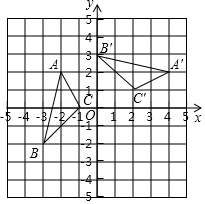
 如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )
如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )| A. | (0,1) | B. | (0,-1) | C. | C(1,-1) | D. | (1,0) |
分析 连接AA′,CC′,线段AA′、CC′的垂直平分线的交点就是点P.
解答 解:连接AA′、CC′,
作线段AA′的垂直平分线MN,作线段CC′的垂直平分线EF,
直线MN和直线EF的交点为P,点P就是旋转中心.
∵直线MN为:x=1,
设直线CC′为y=kx+b,由题意:$\left\{\begin{array}{l}{-k+b=0}\\{2k+b=1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=\frac{1}{3}}\end{array}\right.$,
∴直线CC′为y=$\frac{1}{3}$x+$\frac{1}{3}$,
∵直线EF⊥CC′,经过CC′中点($\frac{1}{2}$,$\frac{1}{2}$),
∴直线EF为y=-3x+2,
由$\left\{\begin{array}{l}{x=1}\\{y=-3x+2}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$,
∴P(1,-1).
故选:C.
点评 本题考查旋转的性质,掌握对应点连线段的垂直平分线的交点就是旋转中心,是解题的关键.


科目:初中数学 来源: 题型:解答题
 小明的手机没电了,现有一个只含A,B,C,D四个同型号插座的插线板(如图,假设每个插座都适合所有的充电插头,且被选中的可能性相同),请计算:
小明的手机没电了,现有一个只含A,B,C,D四个同型号插座的插线板(如图,假设每个插座都适合所有的充电插头,且被选中的可能性相同),请计算:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 一 | 二 | 三 | 四 | 五 | 六 |
| 增减量/辆 | +3 | -2 | -1 | +4 | +2 | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
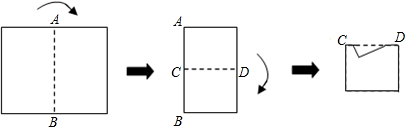
| A. | 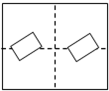 | B. | 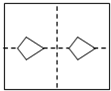 | C. | 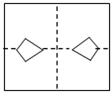 | D. | 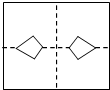 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com