
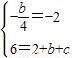 .
.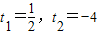 ,∴不动点
,∴不动点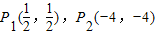 (4分)
(4分)

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:解答题
 米的水管,水管顶端装有一个喷水头,已知喷出的抛物线形水柱在与池中心的水平距离为3米处达到最高高度为
米的水管,水管顶端装有一个喷水头,已知喷出的抛物线形水柱在与池中心的水平距离为3米处达到最高高度为 米,
米, ),水柱的最高点的坐标为(3,
),水柱的最高点的坐标为(3, ),求此坐标系中抛物线对应的函数关系式(不要求写出自变量的取值范围).
),求此坐标系中抛物线对应的函数关系式(不要求写出自变量的取值范围). 水柱落地处刚好在最外轨道上,求当r为多少时,水池中安装的喷水龙头的个数最多?
水柱落地处刚好在最外轨道上,求当r为多少时,水池中安装的喷水龙头的个数最多?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com