
| 时间(秒) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 速度(米/秒) | 0 | 0.3 | 1.3 | 2.8 | 1.9 | 7.6 | 11.0 | 14.1 | 18.4 | 24.2 | 28.9 |
分析 (1)根据表中的数据,即可得出两个变量以及自变量、因变量;
(2)根据时间与速度之间的关系,即可求出v的变化趋势;
(3)根据表中的数据可得出V的变化情况以及在哪1秒钟,V的增加最大;
(4)根据小汽车行驶速度的上限为120千米/小时,再根据时间与速度的关系式即可得出答案;
解答 解:(1)上表反映了时间与速度之间的关系,时间是自变量,速度是因变量;
(2)如果用T表示时间,V表示速度,那么随着T的变化,V的变化趋势是V随着T的增大而增大;
(3)当T每增加1秒,V的变化情况不相同,在第9秒时,V的增加最大;
(4)$\frac{120×1000}{3600}$(米/秒),
由33.3-28.9=4.4,且28.9-24.2=4.7>4.4,
所以估计大约还需1秒.
点评 此题考查的知识点是:函数的表示方法,常量与变量;在解题时要根据表中的数据找出时间与速度之间的关系式是本题的关键.


科目:初中数学 来源: 题型:解答题
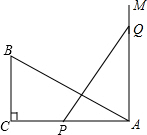 如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=5cm.一条线段PQ=AB,并且P、Q两点分别在线段AC和过A点且垂直于AC的射线AM上运动.问当P点位于AC的什么位置时由P、Q、A点构成的三角形与△ABC全等?并说明理由.
如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=5cm.一条线段PQ=AB,并且P、Q两点分别在线段AC和过A点且垂直于AC的射线AM上运动.问当P点位于AC的什么位置时由P、Q、A点构成的三角形与△ABC全等?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 对于平面直角坐标系中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.己知P(1,2),Q(4,2).
对于平面直角坐标系中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.己知P(1,2),Q(4,2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
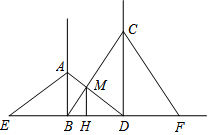 如图,工地上两根电灯杆相距a米,分别在高为4米、6米的A、C处用铁丝将两杆固定,则铁丝AD与铁丝BC的交点M处离地面米的高MH=$\frac{12}{5}$m.
如图,工地上两根电灯杆相距a米,分别在高为4米、6米的A、C处用铁丝将两杆固定,则铁丝AD与铁丝BC的交点M处离地面米的高MH=$\frac{12}{5}$m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
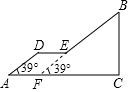 如图,人行天桥的引桥由楼梯和一段水平平台构成,楼梯AD与地面成39°,DE∥AC,楼梯EB与水平地面成39°角,已知BC=6m,AC=11m.
如图,人行天桥的引桥由楼梯和一段水平平台构成,楼梯AD与地面成39°,DE∥AC,楼梯EB与水平地面成39°角,已知BC=6m,AC=11m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com