
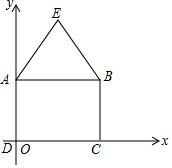
 如图所示,在长方形ABCD中,已知AB=6,AD=4,在长方形ABCD外画△ABE,使AE=BE=5,请建立适当的平面直角坐标系,并求出各顶点的坐标.
如图所示,在长方形ABCD中,已知AB=6,AD=4,在长方形ABCD外画△ABE,使AE=BE=5,请建立适当的平面直角坐标系,并求出各顶点的坐标. 分析 根据矩形的性质即可直接写出矩形的顶点坐标,作EG⊥CD交AB于点F,利用三线合一定理以及勾股定理求得AF和EF的长,则E的坐标即可求得.
解答  解:A的坐标是(0,4),B的坐标是(6,4),C的坐标是(6,0),D的坐标是(0,0);
解:A的坐标是(0,4),B的坐标是(6,4),C的坐标是(6,0),D的坐标是(0,0);
作EG⊥CD交AB于点F.
∵AE=BE,
∴AF=$\frac{1}{2}$AB=$\frac{1}{2}$×6=3,
在直角△AEF中,EF=$\sqrt{A{E}^{2}-A{F}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
则EG=3+4=7,
则E的坐标是(3,7).
点评 本题考查了等腰三角形的性质以及矩形的性质,把求坐标的问题转化为求线段长是问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2017届湖南津市中考数学模拟试卷(2)(解析版) 题型:单选题
下列运算正确的是( )
A. a3+ a3= a6 B. 5a5-a5=4a5 C. (2a)3=6a3 D. a8÷a2= a4
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省南充市度上学期八年级第二次月考数学试卷(解析版) 题型:填空题
计算:(直接写结果) = _____ ,(x+2y﹣3)(x﹣2y+3) = ___________
= _____ ,(x+2y﹣3)(x﹣2y+3) = ___________
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 男生序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
| 身高x(cm) | 163 | 171 | 173 | 156 | 161 | 174 | 164 | 166 | 169 | 164 |
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 勾股定理是世界上最伟大的定理之一,是用代数思想解决几何问题的重要工具,也是数形结合的纽带,周老师在上八年级《从勾股定理到图形面积关系的拓展》一节拓展课时,教学环节清晰,内容安排有序,问题设计合理(如下),作为课堂主人的你,请积极思考解决下列问题:
勾股定理是世界上最伟大的定理之一,是用代数思想解决几何问题的重要工具,也是数形结合的纽带,周老师在上八年级《从勾股定理到图形面积关系的拓展》一节拓展课时,教学环节清晰,内容安排有序,问题设计合理(如下),作为课堂主人的你,请积极思考解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当x=-$\frac{3}{4}$时取得最大值为$\frac{23}{8}$ | B. | 当x=-$\frac{3}{4}$时取得最小值为$\frac{23}{8}$ | ||
| C. | 当x=$\frac{3}{4}$时取得最大值为$\frac{23}{8}$ | D. | 当x=$\frac{3}{4}$时取得最小值为$\frac{23}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com