
【题目】某商店进行店庆活动,决定购进甲、乙两种纪念品,若购进甲种纪念品1件,乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需要280元.
(1)购进甲乙两种纪念品每件各需要多少元?
(2)该商场决定购进甲乙两种纪念品100件,并且考虑市场需求和资金周转,用于购买这些纪念品的资金不少于6300元,同时又不能超过6430元,则该商场共有几种进货方案?
(3)若销售每件甲种纪念品可获利30元,每件乙种纪念品可获利12元,在第(2)问中的各种进货方案中,哪种方案获利最大?最大利润是多少元?
【答案】(1)购进甲乙两种纪念品每件各需要80元和40元;(2)共有3种进货方案;(3)则购进甲种纪念品60件,购进乙种纪念品40件时,可获最大利润,最大利润是2280元.
【解析】试题分析: (1)设购进甲乙两种纪念品每件各需要x元和y元,根据购进甲种纪念品1件,乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需要280元列出方程,求出x,y的值即可;
(2)设购进甲种纪念品a件,则乙种纪念品(100-a)件,根据购进甲乙两种纪念品100件和购买这些纪念品的资金不少于6300元,同时又不能超过6430元列出不等式组,求出a的取值范围,再根据a只能取整数,得出进货方案;
(3)根据实际情况计算出各种方案的利润,比较即可.
试题解析:
(1)设购进甲乙两种纪念品每件各需要x元和y元,根据题意得:
![]() 解得
解得![]()
答:购进甲乙两种纪念品每件各需要80元和40元;
(2) 设购进甲种纪念品a件,则乙种纪念品(100-a)件,根据题意得:
![]()
解得:![]() ,
,
所以a=58或59或60.
所以共有三种方案,分别为
方案1:购进甲种纪念品58件,则购进乙种纪念品42件;
方案2:购进甲种纪念品59件,则购进乙种纪念品41件;
方案3:购进甲种纪念品60件,则购进乙种纪念品40件;
(3) 因为甲种纪念品获利最高,
所以甲种纪念品的数量越多总利润越高,
因此选择购进甲种纪念品60件,购进乙种纪念品40件利润最高,
总利润=60×30+40×12=2280(元)
则购进甲种纪念品60件,购进乙种纪念品40件时,可获最大利润,最大利润是2280元.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 的面积为1.分别倍长(延长一倍)
的面积为1.分别倍长(延长一倍)![]() ,BC,CA得到
,BC,CA得到![]() .再分别倍长A1B1,B1C1,C1A1得到
.再分别倍长A1B1,B1C1,C1A1得到![]() .…… 按此规律,倍长2018次后得到的
.…… 按此规律,倍长2018次后得到的![]() 的面积为( )
的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;
(3)在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出x的值大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一拱形公路桥,圆弧形桥拱的水面跨度AB=80 m,桥拱到水面的最大高度为20 m.(1)求桥拱的半径.
(2)现有一艘宽60 m,顶部截面为长方形且高出水面9 m的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
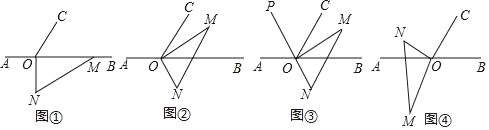
【题目】如图①,点O为直线AB上一点,过点O作射线OC,使∠AOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图①中的三角板OMN摆放成如图②所示的位置,使一边OM在∠BOC的内部,当OM平分∠BOC时,∠BON= ;(直接写出结果)
(2)在(1)的条件下,作线段NO的延长线OP(如图③所示),试说明射线OP是∠AOC的平分线;
(3)将图①中的三角板OMN摆放成如图④所示的位置,请探究∠NOC与∠AOM之间的数量关系.(直接写出结果,不须说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知: 两直线![]() ,
,![]() ,且
,且![]() ∥CD,点
∥CD,点![]() ,
,![]() 分别在直线
分别在直线![]() ,
,![]() 上. 放置一个足够大的三角尺,使得三角尺的两边
上. 放置一个足够大的三角尺,使得三角尺的两边![]() ,
,![]() 分别经过点
分别经过点![]() ,
,![]() . 过点
. 过点![]() 作射线
作射线![]() ,使得
,使得![]() .
.
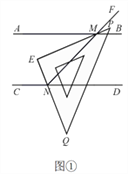
(1)转动三角尺,如图①所示,当射线![]() 与
与![]() 重合,
重合,![]() 时,则
时,则![]() ________;
________;
(2)转动三角尺,如图②所示,当射线![]() 与
与![]() 不重合,
不重合,![]() 时,求
时,求![]() 的度数.
的度数.
(3)转动直角三角尺的过程中, 请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国出租车的收费标准因地而异,济宁市规定:起步价为6元,3千米之后每千米1.4元;济南市规定:起步价8元,3千米之后每千米1.2元.
(1)求济宁的李先生乘出租车2千米,5千米应付的车费;
(2)写出在济宁乘出租车行x千米时应付的车费;
(3)当行驶路程超过3千米,不超过l3千米时,求在济南、济宁两地坐出租车的车费相差多少?
(4)如果李先生在济南和济宁乘出租车所付的车费相等,试估算出李先生乘出租车多少千米(直接写出答案,不必写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有4个大小、质地都相同的乒乓球,球面上分别标有数字1、2、3、4.
(1)搅匀后从中任意摸出1个球,求摸出的乒乓球球面上数字为1的概率;
(2)搅匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,求2次摸出的乒乓球球面上数字之和为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
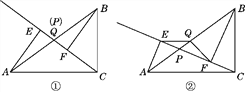
【题目】已知点P是Rt△ABC斜边AB上一动点(不与点A,B重合),分别过点A,B向直线CP作垂线,垂足分别为点E,F,点Q为斜边AB的中点.
(1)如图①,当点P与点Q重合时,AE与BF的位置关系是________,QE与QF的数量关系是________;
(2)如图②,当点P在线段AB上且不与点Q重合时,试判断QE与QF的数量关系,并说明理由.
(温馨提示:直角三角形斜边上的中线等于斜边的一半)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com