
 的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于
的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于 ,其中正确的个数有( )
,其中正确的个数有( )
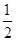 |xD|?|yD|=
|xD|?|yD|=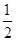 k,同理可求得△CEF的面积也是
k,同理可求得△CEF的面积也是 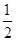 k,因此两者的面积相等;若两个三角形都以EF为底,那么它们的高相同,即E、F到AD的距离相等,由此可证得CD∥EF,然后根据这个条件来逐一判断各选项的正误.
k,因此两者的面积相等;若两个三角形都以EF为底,那么它们的高相同,即E、F到AD的距离相等,由此可证得CD∥EF,然后根据这个条件来逐一判断各选项的正误.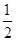 DF?OF=
DF?OF=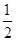 |xD|?|
|xD|?|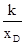 |=
|=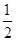 k,
k,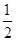 k,故⑤正确;
k,故⑤正确;

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源:不详 题型:单选题
 表示父亲和学子在行进中离家的距离,横轴t表示离家的时间,那么下面与上述诗意大致相吻的图象是
表示父亲和学子在行进中离家的距离,横轴t表示离家的时间,那么下面与上述诗意大致相吻的图象是 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com