
【题目】某宾馆有若千间标准客房,当房价为200元/间时,日均入住数为60间.市场调查表明,在物价局核定的每间标准房价格在160~220元之间(含160元,220元)浮动时,每提高10元,日均入住数减少10间.在不考虑其他因素的前提下,设标准房的价格为x元/间,日均入住数为y间. .
(1) y关于x的解析式为_ .
(2)当标准房的价格定为多少元时,客房的日营业额为10500元?
(3)当标准房的价格定为多少元时,客房的日营业额最大,最大为多少元?
【答案】(1)![]() ;(2)210元;(3)当x=160时,w的最大值为16000元.
;(2)210元;(3)当x=160时,w的最大值为16000元.
【解析】
(1)根据房价每提高10元,日均入住数减少10间列关系式即可;
(2)根据日营业额=房价×入住间数,列出方程求解即可;
(3)根据日营业额=房价×入住间数列出函数关系式,利用二次函数的性质求解即可.
解:(1)由题意得:![]() ;
;
(2)由题意得:x(﹣x+260)=10500,
解得:x1=210,x2=50,
又∵![]() ,
,
∴ x= 210,
答:当标准房的价格定为210元时,客房的日营业额为10500元;
(3)设客房的日营业总额为w,
由题意得:![]() ,
,
∵a=﹣1<0,
∴在160≤x≤220的范围内,w随x的增大而减小,
∴当x=160时,客房的日营业额最大,最大值为16000元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,分别以
,分别以![]() 所在的直线为
所在的直线为![]() 轴、
轴、![]() 轴,建立如图所示的平面直角坐标系,连接
轴,建立如图所示的平面直角坐标系,连接![]() ,反比例函数
,反比例函数![]() 的图象经过线段
的图象经过线段![]() 的中点
的中点![]() ,并与矩形的两边交于点
,并与矩形的两边交于点![]() 和点
和点![]() ,直线
,直线![]() 经过点
经过点![]() 和点
和点![]() .
.
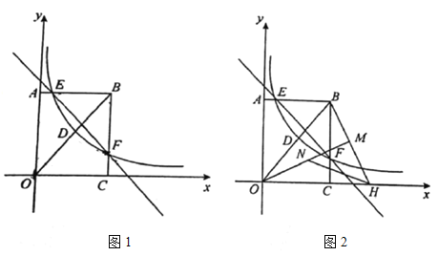
(1)连接![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
(2)如图2,将线段![]() 绕点
绕点![]() 顺时针旋转—定角度,使得点
顺时针旋转—定角度,使得点![]() 的对应点
的对应点![]() 好落在
好落在![]() 轴的正半轴上,连接
轴的正半轴上,连接![]() ,作
,作![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点,求
上的一个动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中
中![]() ,点
,点![]() 从点
从点![]() 运动到点
运动到点![]() 停止,连接
停止,连接![]() ,以
,以![]() 长为直径作
长为直径作![]() .
.
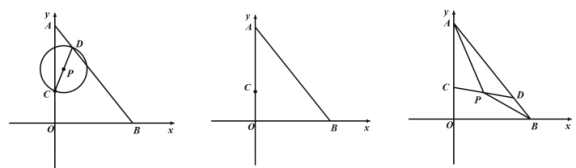
(1)若![]() ,求
,求![]() 的半径;
的半径;
(2)当![]() 与
与![]() 相切时,求
相切时,求![]() 的面积;
的面积;
(3)连接![]() ,在整个运动过程中,
,在整个运动过程中,![]() 的面积是否为定值,如果是,请直接写出面积的定值,如果不是,请说明理由.
的面积是否为定值,如果是,请直接写出面积的定值,如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD内接于⊙O,∠DAB=90°.
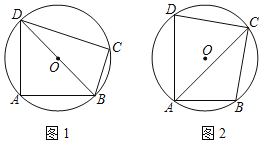
(Ⅰ)如图1,连接BD,若⊙O的半径为6,弧AD=弧AB,求AB的长;
(Ⅱ)如图2,连接AC,若AD=5,AB=3,对角线AC平分∠DAB,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙、丁从笔试、面试两个方面进行量化考核.甲、乙、丙、丁两项得分如下表:(单位:分)
甲 | 乙 | 丙 | 丁 | |
笔试 |
|
|
|
|
面试 |
|
|
|
|
(1)这![]() 名选手笔试成绩的中位数是____________分,面试的众数是_____________分;
名选手笔试成绩的中位数是____________分,面试的众数是_____________分;
(2)该公司规定:笔试、面试分别按![]() ,
,![]() 的比例计总分,请比较甲、乙的总分的大小.
的比例计总分,请比较甲、乙的总分的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平面直角坐标系
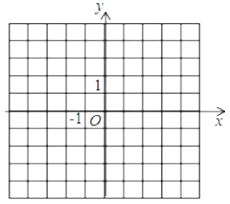
(1)请在图中用描点法画出二次函数y=-![]() x2+2x+1的图象;
x2+2x+1的图象;
(2)计算图象与坐标轴的交点,顶点坐标,写出对称轴;
(3)指出当x≤-3时,y随x的增大而增大还是y随x的增大而减少;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,反比例函数和二次函数y=a(x2+x﹣1)的图象交于点A(1,a)和点B(﹣1,﹣a).
(1)求直线AB与y轴的交点坐标;
(2)要使上述反比例函数和二次函数在某一区域都是y随着x的增大而增大,求a应满足的条件以及x的取值范围;
(3)设二次函数的图象的顶点为Q,当Q在以AB为直径的圆上时,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
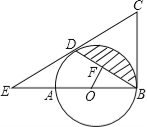
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求解一元一次方程,需要根据等式的基本性质,把方程转化为![]() 的形式;求解二元一次方程组,需要通过消元把它转化为一元一次方程来解;求解三元一次方程组,要把它转化为二元一次方程组来解;求解一元二次方程,需要把它转化为连个一元一次方程来解;求解分式方程,需要通过去分母把它转化为整式方程来解;各类方程的解法不尽相同,但是它们都用到一种共同的基本数学思想——转化,即把未知转化为已知来求解.
的形式;求解二元一次方程组,需要通过消元把它转化为一元一次方程来解;求解三元一次方程组,要把它转化为二元一次方程组来解;求解一元二次方程,需要把它转化为连个一元一次方程来解;求解分式方程,需要通过去分母把它转化为整式方程来解;各类方程的解法不尽相同,但是它们都用到一种共同的基本数学思想——转化,即把未知转化为已知来求解.
用“转化”的数学思想,我们还可以解一些新的方程.
例如,解一元三次方程![]() ,通过因式分解把它转化为
,通过因式分解把它转化为![]() ,通过解方程
,通过解方程![]() 和
和![]() ,可得原方程
,可得原方程![]() 的解.
的解.
再例如,解根号下含有来知数的方程:![]() ,通过两边同时平方把它转化为
,通过两边同时平方把它转化为![]() ,解得:
,解得:![]() . 因为
. 因为![]() ,且
,且![]() ,所以
,所以![]() 不是原方程的根,
不是原方程的根,![]() 是原方程的解.
是原方程的解.
(1)问题:方程![]() 的解是
的解是![]() ,
,![]() __________,
__________,![]() __________;
__________;
(2)拓展:求方程![]() 的解.
的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com