
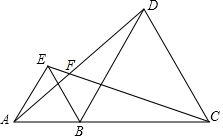
 如图所示,点A,B,C在同一条直线上,△ABE和△BCD都是等边三角形(等边三角形每个内角都是60°).
如图所示,点A,B,C在同一条直线上,△ABE和△BCD都是等边三角形(等边三角形每个内角都是60°).分析 (1)根据题意和等边三角形的性质可以解答本题;
(2)根据题意可以证明△ABD≌△EBC,从而可以解答本题;
(3)根据(2)中的结论可以解答本题.
解答 解:(1)∵△ABE和△BCD都是等边三角形,
∴∠ABE=60°,∠DBC=60°,
∴∠ABD=180°-∠DBC=120°,∠EBC=180°-∠ABE=120°,
故答案为:120°,120°;
(2)线段AD和线段EC相等,
理由:∵△ABE和△BCD都是等边三角形,
∴AB=EB,BD=BC,
∵∠ABD=∠EBC,
∴△ABD≌△EBC(SAS),
∴AD=EC;
(3)由(2)知△ABD≌△EBC,
∴∠DAB=∠CEB,
∵∠CEB+∠ECB=180°-∠EBC=60°,
∴∠DAB+∠ECB=60°,
即∠FAC+∠FCB=60°,
∴∠AFC=120°,
故答案为:120°.
点评 本题考查全等三角形的判定与性质、等边三角形的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用三角形全等的知识解答.


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题
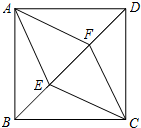 如图,在正方形ABCD中,点E、F在对角线BD上,且BE=EF=FD,连接AF、AE、CE、CF,请你判断四边形AECF的形状,并证明你的结论.
如图,在正方形ABCD中,点E、F在对角线BD上,且BE=EF=FD,连接AF、AE、CE、CF,请你判断四边形AECF的形状,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
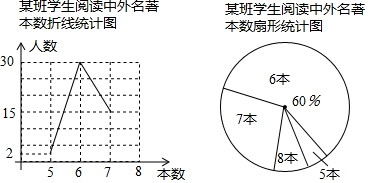
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ②④ | C. | ①③ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (6,7) | B. | (7,8) | C. | (7,9) | D. | (6,9) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com