练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．一个底面为正三角形，侧棱与底面垂直的棱柱，其三视图如图所示，则这个棱柱的体积为36$\sqrt{3}$．

    分析 由三视图判断几何体为三棱柱，把相关数据代入体积公式计算可得答案．

    解答 解：三视图复原的几何体是三棱柱，底面是正三角形，则边长为6，高为3$\sqrt{3}$，
    由三视图可得棱柱高为4，
    它的体积：V=Sh=$\frac{1}{2}$×6×3$\sqrt{3}$×4=36$\sqrt{3}$；
    故答案为：36$\sqrt{3}$．

    点评 本题考查了由三视图判断几何体，用到的知识点是三棱柱的体积公式，关键是判断三视图的数据所对应的几何量．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

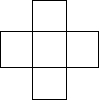    20．如图是一个由5个相同的正方形组成的十字形的纸片，把这一纸片沿一条直线裁成两部分，然后把其中的一部分再沿着另一条直线截成两部分，使所得的三部分纸片通过适当的拼接能组成两个并列的全等的正方形．请在图中画出分割线及拼接后的图形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．把一个绝对值大于10的数表示成a×10n的形式，其中a是整数位数只一位的数，n是正整数，我们把这种表示数的方法叫做科学记数法．即对于大数N，可以表示成N=a×10n的形式，其中1≤a＜10，正整数n为整数数位减1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．解方程：$\frac{1}{x-4}$+$\frac{4}{x-1}$=$\frac{2}{x-3}$+$\frac{3}{x-2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知方程组$\left\{\begin{array}{l}{3x+5y=k+2}\\{2x+3y=k}\end{array}\right.$的解也是方程2x-y=4的解，求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．阅读下面的材料并回答问题：如图1，用两种不同的方法去计算长方形的面积，就得到一条代数恒等式：（a+2b）（a+b）=a2+3ab+2b2，等号左右两边都表示长方形的面积．

    （1）请写出图2中所表示的代数恒等式；
    （2）如图3，由1个立方体A、3个长方体B、2个长方体C拼成一个大长方体，由此可得因式分解a3+3a2b+2ab2=a（a+2b）（a+b）；
    （3）用（2）中的若干个小立方体、长方体拼成的另一个大长方体的长、宽、高分别为2a、a+b、2a+b（a≠b），且体积正好是（2）中大长方体体积的n倍（n为正整数），求n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

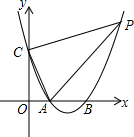    6．如图，抛物线y=x2-4x+3与x轴交于A，B两点，与y轴交于点C，点P在第一象限的抛物线上，且在对称轴右边，S△PAC=10，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．已知D、E分别在△ABC的边AB、AC上，DE∥BC，且AD：DB=2：3，试用向量$\overrightarrow{DE}$表示向量$\overrightarrow{BC}$=$\frac{5}{2}$$\overrightarrow{DE}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′处，∠AE D′=40°，则∠EFB=70°．

    查看答案和解析>>

    同步练习册答案