
 在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1,、…、正方形AnBnCnCn-1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则△A2017A2018B2017的面积是24031.
在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1,、…、正方形AnBnCnCn-1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则△A2017A2018B2017的面积是24031. 分析 根据一次函数图象上点的坐标特征找出A1、A2、A3、A4的坐标,结合图形即可得知点Bn是线段CnAn+1的中点,由此即可得出点Bn的坐标,然后根据三角形的面积公式即可得到结论.
解答 解:观察,发现:A1(1,0),A2(2,1),A3(4,3),A4(8,7),A5(16,15),A6(32,31),…,
∴An(2n-1,2n-1-1)(n为正整数).
观察图形可知:点Bn是线段CnAn+1的中点,
∴点Bn的坐标是(2n-1,2n-1),An(2n-1,2n-1-1)(n为正整数),
∴△AnAn+1Bn的面积是$\frac{1}{2}$(2n-1)2=22n-3,
∴△A2017A2018B2017的面积=22×2017-3=24031,
故答案为:24031.
点评 本题考查了一次函数图象上点的坐标特征以及规律型中点的坐标的变化,根据点的坐标的变化找出变化规律“An(2n-1,2n-1-1)(n为正整数)”是解题的关键.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
 如图所示,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
如图所示,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
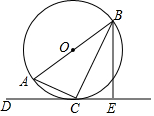 AB是⊙O的直径,CD切⊙O于点C,BE⊥CD于E,连接AC、BC.
AB是⊙O的直径,CD切⊙O于点C,BE⊥CD于E,连接AC、BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
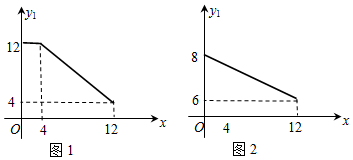
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
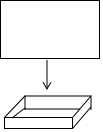 工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)
工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
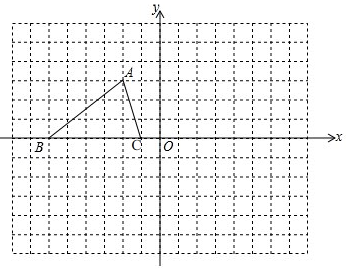 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
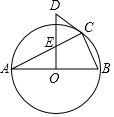 如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.
如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com