
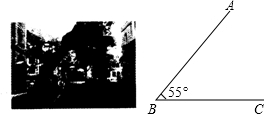
 如图,小区内斜向马路的大树与地面的夹角∠ABC为55°,高为3.2米的大型客车靠近此树的一侧至少要离此树的根部B点多少米才能安全通过?(结果精确到0.1米)
如图,小区内斜向马路的大树与地面的夹角∠ABC为55°,高为3.2米的大型客车靠近此树的一侧至少要离此树的根部B点多少米才能安全通过?(结果精确到0.1米) 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:选择题
 甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图,
甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图,| 用水量(吨) | 4 | 5 | 6 | 9 |
| 户数 | 4 | 5 | 2 | 1 |
| A. | 甲组比乙组大 | B. | 甲、乙两组相同 | C. | 乙组比甲组大 | D. | 无法判断 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=ax2+bx+c,其中2a=b>0>c,且a+b+c=0.
已知抛物线y=ax2+bx+c,其中2a=b>0>c,且a+b+c=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
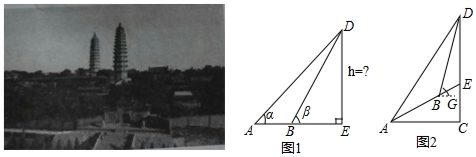
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
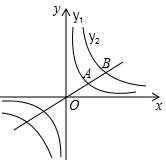 如图,过原点O的直线与反比例函数y1、y2的图象在第一象限内分别交于点A、B,且A为OB的中点.若点B的坐标为(8,2),则y1与x的函数表达式是y1=$\frac{4}{x}$.
如图,过原点O的直线与反比例函数y1、y2的图象在第一象限内分别交于点A、B,且A为OB的中点.若点B的坐标为(8,2),则y1与x的函数表达式是y1=$\frac{4}{x}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com