
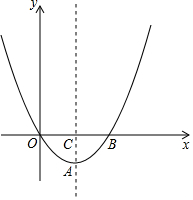
 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćOĪŖ×ų±źŌµć£¬Å×ĪļĻßy=ax2-4ax£Øa”Ł0£©µÄ¶Ō³ĘÖį½»Å×ĪļĻßÓŚAµć£¬½»xÖįÓŚCµć£¬ĒŅAC=OC£®
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćOĪŖ×ų±źŌµć£¬Å×ĪļĻßy=ax2-4ax£Øa”Ł0£©µÄ¶Ō³ĘÖį½»Å×ĪļĻßÓŚAµć£¬½»xÖįÓŚCµć£¬ĒŅAC=OC£®·ÖĪö £Ø1£©ĻČĒóµĆÅ×ĪļĻߵĶŌ³ĘÖį·½³Ģ£¬Č»ŗóŅĄ¾ŻAC=OCæɵƵ½µćAµÄ×ų±ź£¬½«µćAµÄ×ų±ź“śČėÅ×ĪļĻߵĽāĪöŹ½æÉĒóµĆaµÄÖµ£»
£Ø2£©ĻČĒóµĆµćQĖłŌŚÖ±ĻߵĽāĪöŹ½£¬Č»ŗóÖ¤Ć÷OA”ĪµćQĖłŌŚµÄÖ±Ļߣ¬¹żµćP×÷PD”ĪxÖį£¬ĻČÖ¤Ć÷”÷PQDĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬Č»ŗóæÉĒóµĆDPµÄ³¤£¬ÉčµćPµÄ×ų±źĪŖ£Øt£¬$\frac{1}{2}$t2-2t£©£¬æÉĒóµĆµćDµÄ×ų±ź£¬Č»ŗóŅĄ¾ŻDP=14ĮŠ·½³ĢĒó½ā¼“æÉ£»
£Ø3£©ÉčµćEµÄ×ų±źĪŖ£Øt£¬$\frac{1}{2}$t2-2t£©£®Č»ŗóĒóµĆÖ±ĻßAEµÄ½āĪöŹ½£¬Č»ŗóŌŁĒóµĆµćFµÄ×ų±ź£¬½ÓĻĀĄ“£¬Ö¤Ć÷PF=EF£¬Č»ŗóŅĄ¾ŻPF=EFĮŠ³ö¹ŲÓŚtµÄ·½³ĢæÉĒóµĆtµÄÖµ£¬“Ó¶ųµĆµ½µćFµÄ×ų±ź£¬×īŗóŅĄ¾ŻĮ½µć¼äµÄ¾ąĄė¹«Ź½æÉĒóµĆAFµÄÖµ£®
½ā“š ½ā£ŗ£Ø1£©Å×ĪļĻߵĶŌ³ĘÖįĪŖx=-$\frac{-4a}{2a}$=2£¬
”ąC£Ø2£¬0£©£®
”ąOC=2£®
”ßAC=OC£¬
”ąAC=2£®
”ąA£Ø2£¬-2£©£®
½«µćAµÄ×ų±ź“śČėÅ×ĪļĻߵĽāĪöŹ½µĆ£ŗ4a-8a=-2£¬½āµĆ£ŗ-4a=-2£¬½āµĆ£ŗa=$\frac{1}{2}$£¬
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=$\frac{1}{2}$x2-2x£®
£Ø2£©ČēĶ¼1ĖłŹ¾£ŗ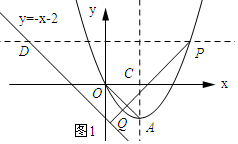
ÉčµćQµÄ×ų±źĪŖ£Øx£¬y£©£®
”ßQ£Øm£¬-m-2£©£¬
”ąx=m£¬y=-m-2£¬
½«x=m“śČėy=-m-2µĆ£ŗy=-x-2£¬
”ąµćQŌŚÖ±Ļßy=-x-2ÉĻ£®
¹żµćP×÷PD”ĪxÖį£¬½»y=-x-2ÓėµćD£®
ÉčOAµÄ½āĪöŹ½ĪŖy=kx£¬½«µćAµÄ×ų±ź“śČėµĆ£ŗ2k=-2£¬½āµĆk=-1£¬
”ąÖ±ĻßOAµÄ½āĪöŹ½ĪŖy=-x£¬
”ąOA”ĪQD£®
”ąPQ”ĶDQ£®
”ą”÷DPQĪŖµČŃüÖ±½ĒČż½ĒŠĪ£®
”ąDP=$\sqrt{2}$QP=14£®
ÉčµćPµÄ×ų±źĪŖ£Øt£¬$\frac{1}{2}$t2-2t£©£¬ŌņµćDµÄׯ×ų±źĪŖ$\frac{1}{2}$t2-2t£®
½«y=$\frac{1}{2}$t2-2t“śČėy=-x-2µĆ-x-2=$\frac{1}{2}$t2-2t£¬½āµĆ£ŗx=-$\frac{1}{2}$t2+2t-2£®
”ąµćDµÄׯ×ų±źĪŖ-$\frac{1}{2}$t2+2t-2£®
”ąPD=t-£Ø-$\frac{1}{2}$t2+2t-2£©=14£¬½āµĆ£ŗt=6»ņt=-4£ØÉįČ„£©£®
”ąµćPµÄ×ų±źĪŖ£Ø6£¬6£©£®
£Ø3£©ČēĶ¼2ĖłŹ¾£ŗ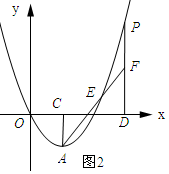
ÉčµćEµÄ×ų±źĪŖ£Øt£¬$\frac{1}{2}$t2-2t£©£®ÉčÖ±ĻßAEµÄ½āĪöŹ½ĪŖy=kx+b£¬½«µćEŗĶµćAµÄ×ų±ź“śČėµĆ£ŗ$\left\{\begin{array}{l}{tk+b=\frac{1}{2}{t}^{2}-2t}\\{2k+b=-2}\end{array}\right.$£¬
½āµĆ£ŗk=$\frac{1}{2}$£Øt-2£©£¬b=-t£¬ŌņÖ±ĻßAEµÄ½āĪöŹ½ĪŖy=$\frac{1}{2}$£Øt-2£©x-t£®
½«x=6“śČėµĆ£ŗy=2t-6£®
”ąF£Ø6£¬2t-6£©£®
”ßAC”ĪDF£¬
”ą”ĻACF=”ĻAFD£®
Ó֔ߔĻCAE=2”ĻPEF£¬
”ą”ĻEFD=2”ĻPEF£®
”ą”ĻPEF=”ĻEPF£®
”ąPF=EF£¬¼“6-£Ø2t-6£©=$\sqrt{£Ø6-x£©^{2}+£Ø6-\frac{1}{2}{t}^{2}+2t£©^{2}}$£¬ÕūĄķµĆ£ŗ£Ø6-t£©2[£Øt-2£©2-6]=0£¬
½āµĆ£ŗt=$\sqrt{6}$+2»ņt=-$\sqrt{6}$+2£ØÉįČ„£©»ņt=0£ØÉįČ„£©£®
µ±t=$\sqrt{6}$+2Ź±£¬F£Ø6£¬2$\sqrt{6}$-2£©£®
”ąAF=$\sqrt{£Ø6-2£©^{2}+£Ø2\sqrt{6}-2+2£©^{2}}$=2$\sqrt{10}$£®
µćĘĄ ±¾ĢāÖ÷ŅŖæ¼²éµÄŹĒ¶ž“ĪŗÆŹżµÄ×ŪŗĻÓ¦ÓĆ£¬ĒóµĆµćAµÄ×ų±źŹĒ½ā“šĪŹĢā£Ø1£©µÄ¹Ų¼ü£¬µĆµ½Čż½ĒŠĪPDQĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬Č»ŗóŅĄ¾ŻPD=14ĮŠ³ö¹ŲÓŚtµÄ·½³ĢŹĒ½ā“šĪŹĢā£Ø2£©µÄ¹Ų¼ü£¬Ö¤µĆFP=FE£¬Č»ŗó¾Ż“ĖĮŠ³ö¹ŲÓŚtµÄ·½³ĢŹĒ½ā“šĪŹĢā£Ø3£©µÄ¹Ų¼ü£®


 Ē§ĄļĀķ×ßĻņ¼ŁĘŚĘŚÄ©·ĀÕęŹŌ¾ķŗ®¼ŁĻµĮŠ“š°ø
Ē§ĄļĀķ×ßĻņ¼ŁĘŚĘŚÄ©·ĀÕęŹŌ¾ķŗ®¼ŁĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | a£¾b£¾c | B£® | c£¾a£¾b | C£® | c£¾b£¾a | D£® | a£¾c£¾b |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | Čż½ĒŠĪµÄÖŠĻß”¢½ĒĘ½·ÖĻߣ¬øßĻ߶¼ŹĒĻ߶Ī | |
| B£® | ÓŠŅ»øöÄŚ½ĒŹĒÖ±½ĒµÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪ | |
| C£® | ČĪŅāČż½ĒŠĪµÄĶā½ĒŗĶ¶¼ŹĒ360”ć | |
| D£® | Čż½ĒŠĪµÄŅ»øöĶā½Ē“óÓŚČĪŗĪŅ»øöÄŚ½Ē |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -1.75 | B£® | -1.5 | C£® | -0.25 | D£® | -1.25 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | m=4£¬n=12 | B£® | m=-4£¬n=12 | C£® | m=-4£¬n=-12 | D£® | m=4£¬n=-12 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | $\frac{1}{2a-6}$ | B£® | $\frac{1}{a-3}$ | C£® | $\frac{1}{2a+6}$ | D£® | $\frac{1}{a+3}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | ÓŠĮ½øöĻąµČµÄŹµŹżøł | B£® | ÓŠĮ½øö²»ĻąµČµÄŹµŹżøł | ||
| C£® | ƻӊŹµŹżøł | D£® | ĪŽ·ØÅŠ¶Ļ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com