
科目:初中数学 来源: 题型:
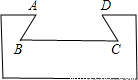
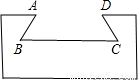
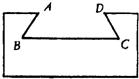 (2001•广州)如图,燕尾槽的横断面是等腰梯形,其中燕尾角∠B=55°,外口宽AD=190mm,燕尾槽的深度是70mm,则它的里口宽BC=
(2001•广州)如图,燕尾槽的横断面是等腰梯形,其中燕尾角∠B=55°,外口宽AD=190mm,燕尾槽的深度是70mm,则它的里口宽BC=查看答案和解析>>
科目:初中数学 来源:2001年全国中考数学试题汇编《圆》(06)(解析版) 题型:解答题
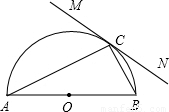
查看答案和解析>>
科目:初中数学 来源:2001年广东省广州市中考数学试卷(解析版) 题型:解答题
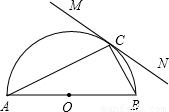
查看答案和解析>>
科目:初中数学 来源:2001年广东省广州市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com