
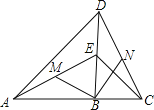
【题目】如图,已知点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点,现有如下结论:①∠ABD=∠BDN;②MB=NB;③MB⊥NB;④S△ABM=S△BCN,其中正确的结论是 (只填序号).
【答案】②③④
【解析】
试题分析:①由三角形内最多只有一个直角得出该结论不成立;
②通过证明△ABE≌△DBC得出AE=DC,根据直角三角形斜边上中线的特点,可得出结论成立;
③通过证明△ABM≌△DBN得出∠DBN=∠ABM,通过等量替换得出结论成立;
④由②中的三角形全等可知其面积也相等,故其面积的一半也相等,结论成立.
解:①∵∠ABD=∠DBC,且点B在线段AC上,
∴∠ABD=∠DBC=180°÷2=90°,
在△BDC中,∠DBC=90°
∴∠BDN=∠BDC<90°(三角形中最多只有一个直角存在),
∴∠ABD≠∠BDN,
即①不成立.
②在直角△ABE与直角△DBC中,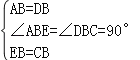 ,
,
∴△ABE≌△DBC(SAS),
∴AE=DC,
又M,N分别是AE,CD的中点,
∴BM=![]() AE,BN=
AE,BN=![]() DC,
DC,
∴BM=BN,
即②成立.
③在△ABM和△DBN中,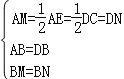 ,
,
∴△ABM≌△DBN,
∴∠DBN=∠ABM,
∴∠MBN=∠MBD+∠DBN=∠MBD+∠ABM=∠ABD=90°,
∴MB⊥NB,
即③成立.
④∵M,N分别是AE,CD的中点,
∴S△ABM=![]() S△ABE,S△BCN=
S△ABE,S△BCN=![]() S△DBC,
S△DBC,
由②得知,△ABE≌△DBC,
∴S△ABM=S△BCN,
即④成立.
故答案为:②③④.


科目:初中数学 来源: 题型:
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边三角形CDE,使点E,A在直线DC同侧,连接AE.求证:

(1)△AEC≌BDC;
(2)AE∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=α(30°<α<45°),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.
(1)如图,当α=40°,且射线OM在∠AOB的外部时,用直尺、量角器画出射线OD,ON的准确位置;
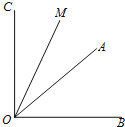
(2)求(1)中∠MON的度数,要求写出计算过程;
(3)当射线OM在∠AOB的内部时,用含α的代数式表示∠MON的度数.(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
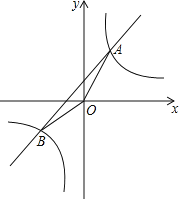
(1)求一次函数与反比例函数的解析式;
(2)求△ABO的面积;
(3)根据所给条件,请直接写出不等式kx+b>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列判断:①在数轴上,原点两旁的两个点所表示的数都是互为相反数;②任何正数必定大于它的倒数;③5ab,![]() ,
,![]() 都是整式;④x2﹣xy+y2是按字母y的升幂排列的多项式,其中判断正确的是( )
都是整式;④x2﹣xy+y2是按字母y的升幂排列的多项式,其中判断正确的是( )
A.①② B.②③ C.③④ D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车同时分别从A、B两城沿同一条高速公路匀速驶向C城.已知A、C两城的距离为360km,B、C两城的距离为320km,甲车比乙车的速度快10km/h,结果两辆车同时到达C城.设乙车的速度为xkm/h.
(1)根据题意填写下表:
行驶的路程(km) | 速度(km/h) | 所需时间(h) | |
甲车 | 360 |
|
|
乙车 | 320 | x |
|
(2)求甲、乙两车的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com