
数学活动——求重叠部分的面积。
问题情境:数学活动课上,老师出示了一个问题:

如图(1),将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合,DE经过点C,DF交AC于点G。
求重叠部分(△DCG)的面积。
(1)独立思考:请解答老师提出的问题。
(2)合作交流:“希望”小组受此问题的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图(2),你能求出重叠部分(△DGH)的面积吗?请写出解答过程。
(3)提出问题:老师要求各小组向“希望”小组学习,将△DEF绕点D旋转,再提出一个求重叠部分面积的问题。“爱心”小组提出的问题是:如图(3),将△DEF绕点D旋转,DE,DF分别交AC于点M,N,使DM=MN,求重叠部分(△DMN)的面积。
任务:①请解决“爱心”小组所提出的问题,直接写出△DMN的面积是 .
②请你仿照以上两个小组,大胆提出一个符合老师要求的问题,并在图中画出图形,标明字母,不必解答(注:也可在图(1)的基础上按顺时针方向旋转)。
解:(1)∵∠ACB=90°,D是AB的中点,∴DC=DB=DA。∴∠B=∠DCB。
又∵△ABC≌△FDE,∴∠FDE=∠B。
∴∠FDE=∠DCB。∴DG∥BC。∴∠AGD=∠ACB=90°。∴DG⊥AC。
又∵DC=DA,∴G是AC的中点。
∴CG=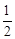 AC=
AC=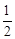 ×8=4,DG=
×8=4,DG=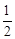 BC=
BC=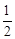 ×6=3。
×6=3。
∴SDCG=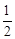 ·CG·DG=
·CG·DG=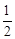 ×4×3=6。
×4×3=6。
(2)∵△ABC≌△FDE,∴∠B=∠1。
∵∠C=90°,ED⊥AB,∴∠A+∠B=90°,∠A+∠2=90°。∴∠B=∠2。
∴∠1=∠2。∴GH=GD。
∵∠A+∠2=90°,∠1+∠3=90°,∴∠A=∠3。∴AG=GD。∴AG=GH。
∴点G是AH的中点。
在Rt△ABC中,AB= 10,
∵D是AB的中点,∴AD=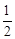 AB=5。
AB=5。
在△ADH与△ACB中,∵∠A =∠A,∠ADH=∠ACB=90°,
∴△ADH∽△ACB。 ∴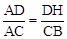 ,即
,即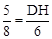 ,解得
,解得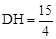 。
。
∴S△DGH=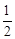 S△ADH=
S△ADH=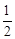 ×
×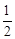 ·DH·AD=
·DH·AD= ×
×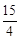 ×5=
×5=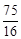 。
。
(3)①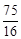 。
。
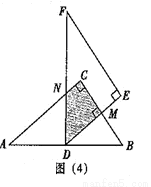
②如图4,将△DEF绕点D旋转,使DE⊥BC于点M,DF交A C于点N,求重叠部分(四边形DMCN)的面积。(答案不唯一)
【解析】
试题分析:(1)通过证明DG是Rt△ABC的中位线,即可求得重叠部分(△DCG)的面积。
(2)通过证明S△DGH=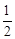 S△ADH,即可求得重叠部分(△DGH)的面积。
S△ADH,即可求得重叠部分(△DGH)的面积。
(3)①如图,将△DEF绕点D旋转至(2)的位置△DE′F′,过点M作MP⊥DM交DE′于点P,过点N作NQ⊥DM交DF′于点Q,则
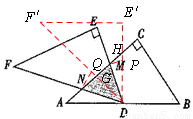
∵∠NDQ=∠QDM(旋转角相等),DM=MN,∠DNQ=∠DQM=90°,
∴△ABC≌△FDE(ASA)。
∴S△DDMN=S△DGH==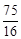 。
。
②开放型(答案不唯一)。


科目:初中数学 来源: 题型:
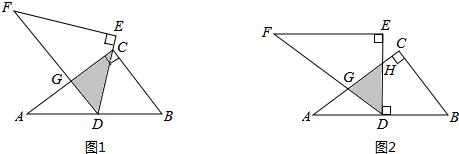
| 75 |
| 16 |
| 75 |
| 16 |

查看答案和解析>>
科目:初中数学 来源:2013年山西省高级中等学校招生考试数学 题型:044
数学活动——求重叠部分的面积.
问题情境:数学活动课上,老师出示了一个问题:
如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合,DE经过点C,DF交AC于点G.求重叠部分(△DCG)的面积.
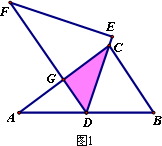
(1)独立思考:请解答老师提出的问题.
(2)合作交流:“希望”小组受此问题的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,你能求出重叠部分(△DGH)的面积吗?请写出解答过程.
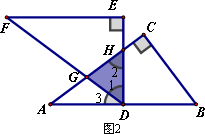
(3)提出问题:老师要求各小组向“希望”小组学习,将△DEF绕点D旋转,再提出一个求重叠部分面积的问题.“爱心”小组提出的问题是:如图3,将△DEF绕点D旋转,DE,DF分别交AC于点M,N,使DM=MN求重叠部分(△DMN)的面积、
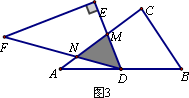
任务:①请解决“爱心”小组所提出的问题,直接写出△DMN的面积是________.
②请你仿照以上两个小组,大胆提出一个符合老师要求的问题,并在图中画出图形,标明字母,不必解答(注:也可在图(1)的基础上按顺时针方向旋转).
查看答案和解析>>
科目:初中数学 来源:2013年山西省太原市中考数学试卷(解析版) 题型:解答题


查看答案和解析>>
科目:初中数学 来源:2013年山西省中考数学试卷(解析版) 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com