
【题目】如图1,正方形ABCD中,点E是BC延长线上一点,连接DE,过点B作BF⊥DE于点F,连接FC
.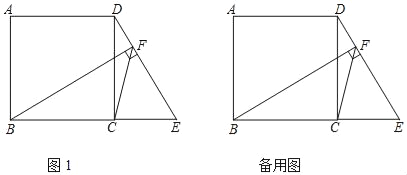
(1)求证:∠FBC=∠CDF.
(2)作点C关于直线DE的对称点G,连接CG,FG.
①依据题意补全图形;
②用等式表示线段DF,BF,CG之间的数量关系并加以证明.
【答案】(1)见解析;(2) ①见解析;②BF=DF+CG,理由见解析.
【解析】分析:(1)由∠FBC+∠COB=90°,∠CDF+∠DOF=90°,根据等角的余角相等证明即可;
(2)①根据题意画出图形即可;②结论:BF=DF+CG.利用截长补短法,构造相似三角形解决问题即可;
详解:(1)证明:如图1中,设CD交BF于点O.
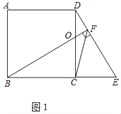
∵四边形ABCD是正方形,
∴∠BCO=90°,
∵BF⊥DE,
∴∠OFD=∠OCB=90°,
∴∠FBC+∠COB=90°,∠CDF+∠DOF=90°,
∵∠DOF=∠BOC,
∴∠FBC=∠CDF.
(2)解:①如图2中,
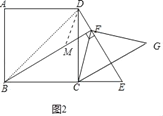
②结论:BF=DF+CG.
理由:在线段FB上截取FM,使得FM=FD.
∵∠BDC=∠MDF=45°,
∴∠BDM=∠CDF,
∵![]() =
=![]() =
=![]() ,
,
∴△BDM∽△CDF,
∴![]() =
=![]() =
=![]() ,∠DBM=∠DCF,
,∠DBM=∠DCF,
∴BM=![]() CF,
CF,
∴∠CFE=∠FCD+∠CDF=∠DBM+∠BDM=∠DMF=45°,
∴∠EFG=∠EFC=45°,
∴∠CFG=90°,
∵CF=FG,
∴CG=![]() CF,
CF,
∴BM=CG,
∴BF=BM+FM=CG+DF.


科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一方队正沿箭头所指的方向前进

(1)A的位置为第三列第四行,表示为(3,4),那么B的位置是____________.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(2)B左侧第二个人的位置是____________.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(3)如果队伍向东前进,那么A北侧第二个人的位置是____________.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(4)![]() 表示的位置是____________.
表示的位置是____________.
A.A B.B C.C D.D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )

A. 2![]() B. 3
B. 3![]() C. 6
C. 6![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把边长为2的等边三角形△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于点F.
(1)证明:AC⊥BD;
(2)求线段BD的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明购买了一套安居型商品房,他准备将地面铺上地砖,地面结构如图所示.请根据图中的数据(单位:m),解答下列问题:
(1)用含x、y的代数式表示地面总面积;
(2)若x=5,y=![]() ,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90,AC=BC,AD平分∠CAB,DE⊥AB,垂足为E.
(1)求证:CD=BE;
(2)若AB=10,求BD的长度。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com