
【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26,![]() ).
).

科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;

(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委为积极参与“陶行知杯.全国书法大赛”现场决赛,向学校学生征集书画作品,今年3月份举行了“书画比赛”初赛,初赛成绩评定为A,B,C,D,E五个等级.该校七年级书法班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题.

(1)该校七年级书法班共有 名学生;扇形统计图中C等级所对应扇形的圆心角等于 度,并补全条形统计图;
(2)A等级的4名学生中有2名男生,2名女生,现从中任意选取2名学生参加“陶行知杯.全国书法大赛”现场决赛,请你用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=a.作BC边的三等分点C1,使得CC1∶BC1=1∶2,过点C1作AC的平行线交AB于点A1,过点A1作BC的平行线交AC于点D1,作BC1边的三等分点C2,使得C1C2∶BC2=1∶2,过点C2作AC的平行线交AB于点A2,过点A2作BC的平行线交A1C1于点D2;如此进行下去,则线段AnDn的长度为( )

A. ![]() aB.
aB. ![]() aC.
aC. ![]() aD.
aD. ![]() a
a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在四边形ABCD中,∠A=∠C=90°.
(1)∠ABC+∠ADC= °;
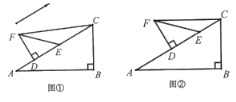
(2)如图①,若DE平分∠ADC,BF平分∠ABC的外角,请写出DE与BF的位置关系,并证明;
(3)如图②,若BE,DE分别四等分∠ABC、∠ADC的外角(即∠CDE=![]() ∠CDN,∠CBE=
∠CDN,∠CBE=![]() ∠CBM),试求∠E的度数.
∠CBM),试求∠E的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种水彩笔,在购买时,若同时额外购买笔芯,每个优惠价为3元,使用期间,若备用笔芯不足时需另外购买,每个5元.现要对在购买水彩笔时应同时购买几个笔芯作出选择,为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据.
水笔支数 | 4 | 6 | 8 | 7 | 5 |
需要更换的笔芯个数x | 7 | 8 | 9 | 10 | 11 |
设x表示水彩笔在使用期内需要更换的笔芯个数,y表示每支水彩笔在购买笔芯上所需要的费用(单位:元),n表示购买水彩笔的同时购买的笔芯个数.
(1)若x=9,n=7,则y= ;若x=7,n=9,则y= ;
(2)若n=9,用含x的的代数式表示y的取值;
(3)假设这30支笔在购买时,每支笔同时购买9个笔芯,或每支笔同时购买10个笔芯,分别计算这30支笔在购买笔芯时所需的费用,以费用最省作为选择依据,判断购买一支水彩笔的同时应购买9个还是10个笔芯?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为( )

A.1B.1.3C.1.2D.1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
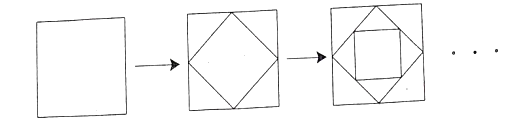
【题目】如图,依次连接边长为1的小正方形各边的中点,得到第二个小正方形,再依次连接第二个小正方形各边的中点得到第三个小正方形,按这样的规律第2019个小正方形的面积为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刘同学在一次课外活动中,用硬纸片做了两个直角三角形,在![]() 中,
中,![]() ,
,![]() ,
,![]() ;在
;在![]() 中,
中,![]() ,
,![]() ,
,![]() .图①是小刘同学所做的一个数学探究:他将
.图①是小刘同学所做的一个数学探究:他将![]() 的直角边
的直角边![]() 与
与![]() 的斜边
的斜边![]() 重合在一起,并将
重合在一起,并将![]() 沿
沿![]() 方向移动.在移动过程中,
方向移动.在移动过程中,![]() 、
、![]() 两点始终在
两点始终在![]() 边上(移动开始时点
边上(移动开始时点![]() 与点
与点![]() 重合).
重合).
(1)在![]() 沿
沿![]() 方向移动的过程中,小刘发现:
方向移动的过程中,小刘发现:![]() 、
、![]() 两点间的距离逐渐 ;连接
两点间的距离逐渐 ;连接![]() 后,
后,![]() 的度数逐渐 .(填“不变”、“变大”或“变小”);
的度数逐渐 .(填“不变”、“变大”或“变小”);
(2)小刘同学经过进一步地研究,编制了如下问题:
问题①:如图②,当![]() 、
、![]() 的连线与
的连线与![]() 平行时,求平移距离
平行时,求平移距离![]() 的长;
的长;
问题②:如图③,在![]() 的移动过程中,
的移动过程中,![]() 的值是否为定值?如果是,请求出此定值;如果不是,请说明理由.
的值是否为定值?如果是,请求出此定值;如果不是,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com