
����Ŀ��ij�о���ʹ������ˮ�����±��շ�(ˮ�Ѱ��½���)��

��1����a=2ʱ��ij�û�һ�������� 28m3ˮ,����û������Ӧ���ɵ�ˮ�ѣ�
��2����ij������ˮ��Ϊm������,�� m��20ʱ,����û�Ӧ���ɵĵ�ˮ��Ϊ________Ԫ(�ú� a��m����ʽ��ʾ)��
��3����a=2ʱ,�ס������û�һ���¹���ˮ 40m3,��֪���û����ɵ�ˮ�ѳ�����24Ԫ,����û��������ˮxm3,����ס������û�һ���¹����ɵ�ˮ��(�ú� x����ʽ��ʾ)��
���𰸡���1�����û������Ӧ���ɵ�ˮ��Ϊ80Ԫ����2��2ma-16a����3���������.
��������
��1�������û���ˮ��������ݲ�ͬ���ۼ�����Ӧ���ɵ�ˮ�ѣ�
��2��������ˮ�������벻ͬ�ĵ��ۣ������Ӧ���ɵ�ˮ�ѣ�
��3�����жϼ�����ˮ�����·�Χ���ٷ���������ۼ��㣮
��1�����û�һ������ˮ28m3������a=2Ԫ��
����ɵã�12��2+��20-12����2��1.5+��28-20����2��2=24+24+32=80��Ԫ��
�𣺸��û������Ӧ���ɵ�ˮ��Ϊ80Ԫ��
��2�����û�һ������ˮm��m��20�������ף�����aԪ��
����ɵã�12��a+��20-12����1.5a+��m-20����2a=12a+12a-40a+2ma=2ma-16a��Ԫ��
�ʴ�Ϊ��2ma-16a��
��3�����û����ɵ�ˮ�ѳ�����24Ԫ��
��x��12��
�ٵ�12��x��20ʱ��
��a=2Ԫ��
����û����ɵ�ˮ�ѣ�2��12+��x-12����2��1.5=3x-12��Ԫ����
����һ���¹���ˮ40�����ף�
������ˮ��20��40-x��28��
�����û����ɵ�ˮ�ѣ�2��12+��20-12����2��1.5+��40-x-20����2��2=128-4x��Ԫ����
��������û������ɵ�ˮ�ѣ�3x-12+128-4x=116-x��Ԫ����
�ڵ�20��x��28ʱ��
��a=2Ԫ��
����û����ɵ�ˮ�ѣ�2��12+��20-12����2��1.5+��x-20����2��2=4x-32��Ԫ����
����һ���¹���ˮ40�����ף�
������ˮ��12��40-x��20��
�����û����ɵ�ˮ�ѣ�2��12+��40-x-12����2��1.5=108-3x��Ԫ����
��������û������ɵ�ˮ�ѣ�4x-32+108-3x=x+76��Ԫ��.
�۵�28��x��40ʱ��
��a=2Ԫ��
����û����ɵ�ˮ�ѣ�2��12+��20-12����2��1.5+��x-20����2��2=4x-32��Ԫ����
����һ���¹���ˮ40�����ף�
������ˮ��0��40-x��12��
�����û����ɵ�ˮ�ѣ���40-x����2=80-2x��Ԫ����
��������û������ɵ�ˮ�ѣ�4x-32+80-2x=2x+48��Ԫ��.
�𣺼������û������ɵ�ˮ�ѣ�
��12��x��20ʱ����ˮ�ѣ�116-x��Ԫ��
��20��x��28ʱ����ˮ�ѣ�x+76��Ԫ��
��28��x��40ʱ����ˮ�ѣ�2x+48��Ԫ.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽�������⣺
��֪��b����С������������a��b���㣨c��5��2+|a+b|��0����ش����⣺
��1����ֱ��д��a��b��c��ֵ��a���� ����b���� ����c���� ����
��2��������a��b��c����������Ӧ�ĵ�ֱ�ΪA��B��C����A��B��Cͬʱ��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��1����λ���Ⱥ�3����λ���ȵ��ٶ������˶�������t���ӹ�������B���C֮��ľ����ʾΪBC����A���B֮��ľ����ʾΪAB����A���C֮��ľ����ʾΪAC��
��t���ӹ���AC�ij���Ϊ�� ������t�Ĺ�ϵʽ��ʾ����
�����ʣ�BC��AB��ֵ�Ƿ�����ʱ��t�ı仯���ı䣿���仯����˵�����ɣ������䣬������ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1=��2��Ҫ�õ���ABD�ա�ACE�������������в�ѡһ�����������ǣ� ��

A��AB=AC B��DB=EC C����ADB=��AEC D����B=��C
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ˮƽ�������мס��ҡ�������Բ���������������㹻�ߣ�������뾶֮��Ϊ![]() ����������ͬ�Ĺ�����������
����������ͬ�Ĺ�����������![]() �߶ȴ���ͨ�������ӵ���������
�߶ȴ���ͨ�������ӵ���������![]() ���������������У�ֻ�м�����ˮ��ˮλ��
���������������У�ֻ�м�����ˮ��ˮλ��![]() ����ͼ��ʾ����ÿ����ͬʱ���Һͱ�ע����ͬ����ˮ����ʼעˮ
����ͼ��ʾ����ÿ����ͬʱ���Һͱ�ע����ͬ����ˮ����ʼעˮ![]() ���ӣ��ҵ�ˮλ����
���ӣ��ҵ�ˮλ����![]() ����ʼע��__________���ӵ�ˮ�������ҵ�ˮλ�߶�֮����
����ʼע��__________���ӵ�ˮ�������ҵ�ˮλ�߶�֮����![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲���ʽ:
![]() ��
��![]() ��
��![]() ��
��![]() ������
������
��1��������㷢�ֵĹ������:7��9+1=________2��
��2���ú�n�ĵ�ʽ��ʾ����Ĺ��ɣ�________��
��3�����ҵ��Ĺ��ɽ����������⣺����:
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������A��B��C������,�ֱ��ʾ������-12��-5��5,����P��A����,��ÿ��1����λ���ٶ����յ�C�ƶ�,���ƶ�ʱ��Ϊ t�롣

��1���ú�t�Ĵ���ʽ��ʾP����A�͵�C�ľ��룺PA=________ �� PC=________��
��2������P�ӵ�A����,���C�ƶ�,��Q��ÿ��3����λ�ӵ�C����,���յ�A�ƶ�,��������������P���Q��������?
��3������P�˶���B��ʱ,��Q��A�����,��ÿ��3����λ���ٶ���C���˶�,Q�㵽��C���,��������ͬ�����ٶȷ���,�˶����յ�A,�ڵ�Q��ʼ�˶���,P��Q����֮��ľ����ܷ�Ϊ2����λ?�����,�������ʱ��P��ʾ�������������,��˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪E��F��ABCD�Խ���AC�ϵ����㣬��BE��AC��DF��AC�� 
��1����֤����ABE�ա�CDF��
��2����д��ͼ�г���ABE�ա�CDF����������ȫ�������Σ��������Ӹ����ߣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ѧУΪ�˴���ȫʡ���������ݡ���������һ��ͼ�飬���п�����ͼ��ƽ��ÿ���ļ۸����ѧ��ͼ��ƽ��ÿ���ļ۸��5Ԫ.��֪ѧУ��12000Ԫ����Ŀ�����ͼ��ı�������9000Ԫ�������ѧ��ͼ��ı�����ȣ���ѧУ����Ŀ�����ͼ�����ѧ��ͼ��ƽ��ÿ���ļ۸���Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�У�AD��BC����ABC=90�㣬�Խ���AC��BD�ཻ�ڵ�O�����������У������ж϶Խ����ഹֱ���ǣ� �� 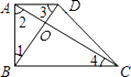
A.��1=��4
B.��1=��3
C.��2=��3
D.OB2+OC2=BC2
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com