
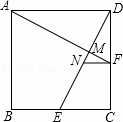
如图,在正方形ABCD中,点E、F分别是BC、CD的中点,DE交AF于点M,点N为DE的中点.
(1)若AB=4,求△DNF的周长及sin∠DAF的值;
(2)求证:2AD•NF=DE•DM.
| (1)解:∵点E、F分别是BC、CD的中点, ∴EC=DF=×4=2, 由勾股定理得,DE= ∵点F是CD的中点,点N为DE的中点, ∴DN=DE=×2 NF=EC=×2=1, ∴△DNF的周长=1+ 在Rt△ADF中,由勾股定理得,AF= 所以,sin∠DAF= (2)证明:在△ADF和△DCE中,
∴△ADF≌△DCE(SAS), ∴AF=DE,∠DAF=∠CDE, ∵∠DAF+∠AFD=90°, ∴∠CDE+∠AFD=90°, ∴AF⊥DE, ∵点E、F分别是BC、CD的中点, ∴NF是△CDE的中位线, ∴DF=EC=2NF, ∵cos∠DAF= cos∠CDE= ∴ ∴2AD•NF=DE•DM. |


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
在平面直角坐标系中,将抛物线y=3x2先向右平移1个单位,再向上平移2个单位,得到的抛物线的解析式是( )
|
| A. | y=3(x+1)2+2 | B. | y=3(x+1)2﹣2 | C. | y=3(x﹣1)2+2 | D. | y=3(x﹣1)2﹣2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
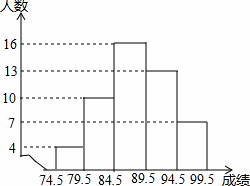
为了了解某地初中三年级学生参加消防知识竞赛成绩(均为整数),从中抽取了1%的同学的竞赛成绩,整理后绘制了如下的频数分布直方图,请结合图形解答下列问题:
(1)指出这个问题中的总体;
(2)求竞赛成绩在84.5﹣89.5这一小组的频率;
(3)如果竞赛成绩在90分以上(含90分)的同学可以获得奖励,请估计该地初三年级约有多少人获得奖励.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com