
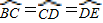 ,∠BAE=90度.
,∠BAE=90度.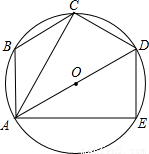
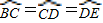 得∠BAC=∠CAD=∠DAE,
得∠BAC=∠CAD=∠DAE, ,即S△ACD=
,即S△ACD= AC×CD=
AC×CD=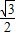 .
.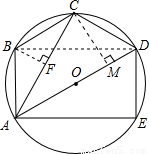 解:(1)∵AD为⊙O的直径,
解:(1)∵AD为⊙O的直径, ,
,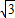 .
. AC×CD=
AC×CD=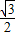 .
. AC=
AC= ,
, ,
, AC×BF=
AC×BF=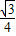 ,
,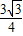 .
.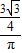 =
=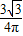 .
.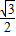 ,
, (BC+AD)CM=
(BC+AD)CM=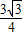 .
.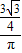 =
=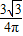 .
.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源:2009年全国中考数学试题汇编《二次函数》(05)(解析版) 题型:解答题
 ,1),B(s,t),C(
,1),B(s,t),C( ,0),抛物线y=x2+mx-m的顶点P是直角梯形OABC内部或边上的一个动点,m为常数.
,0),抛物线y=x2+mx-m的顶点P是直角梯形OABC内部或边上的一个动点,m为常数.
查看答案和解析>>
科目:初中数学 来源:2009年湖北省宜昌市中考数学试卷(解析版) 题型:解答题
 ,1),B(s,t),C(
,1),B(s,t),C( ,0),抛物线y=x2+mx-m的顶点P是直角梯形OABC内部或边上的一个动点,m为常数.
,0),抛物线y=x2+mx-m的顶点P是直角梯形OABC内部或边上的一个动点,m为常数.
查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《圆》(11)(解析版) 题型:解答题
 与
与 是否相等?请你说明理由;
是否相等?请你说明理由;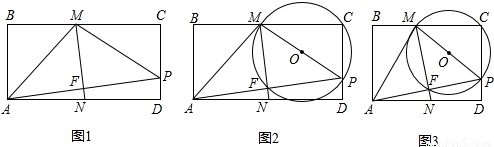
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com