
矩形OABC在平 面直角坐标系中的位置如图所示,A、C两点的坐标分别为A(6,0),C(0,-3),直线y=- x与BC边相交于D点.
x与BC边相交于D点.
(1)若抛物线y=ax- x经过点A,试确定此抛物线的解析式;
x经过点A,试确定此抛物线的解析式;
(2)在(1)中的抛物线的对称轴上取一点E,求出EA+ED的最小值;
(3)设(1)中的抛物线的对称轴与直线OD交于点M,点P为对称轴上一动点,以P、O、M为顶点的三角形与△OCD相似,求符合条件的点P的坐标.
(1)抛物线的解析式为y= x-
x- x (2)EA+ED的最小值为5 (3)P1(3,0),P2(3,4)
x (2)EA+ED的最小值为5 (3)P1(3,0),P2(3,4)
解析试题分析:(1)抛物线y=ax- x经过点A(6,0),
x经过点A(6,0),
∴0=36a- ×36, ∴a=
×36, ∴a= ,故抛物线的解析式为y=
,故抛物线的解析式为y= x-
x- x.
x.
(2)直线y=- x与BC边相交于D点,
x与BC边相交于D点,
当y=-3时,x=4,∴点D的坐标为(4,-3).
∵点O与点A关于对称轴对称,且点E在对称轴上,
∴EA="EO," ∴EA+ED=EO+ED,
则最小值为OD=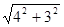 =5,∴EA+ED的最小值为5.
=5,∴EA+ED的最小值为5.
(3)抛物线的对称轴与x轴的交点P1符合条件.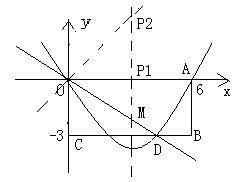
∵OA∥CB ,∴∠P1OM=∠CDO.
∵∠OP1M=∠DCO=90°,∴Rt△P1OM∽Rt△CDO.
∵抛物线的对称轴为x=3,∴点P1的坐标为(3,0).
过点O作OD的垂线交抛物线的对称轴于点P2.
∵对称轴平行于y轴,∴∠P2MO=∠DOC.
∵∠P2OM=∠DCO=90°, ∴Rt△P2MO∽Rt△DOC.
∴点P2也符合条件,∠OP2M=∠ODC.
∵P1O=CO=3,∠P2P1O=∠DCO=90°,
∴Rt△P2P1O ≌Rt△DCO. ∴P1P2=CD=4.
∵点P2在第一象限,∴点P2的坐标为(3,4).
∴符合条件的点P有两个,分别是P1(3,0),P2(3,4).
考点:抛物线,全等三角形
点评:本题考查抛物线,全等三角形,掌握抛物线的性质,要求考生能求函数解析式,熟悉全等三角形的判定方法,并会证明两个三角形全等


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com