
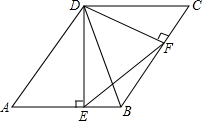
 如图,在?ABCD中,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为点E、F,有下列结论:①AB=2DF;②DE•CF=DF•AE;③∠DFE=∠CDB;④如果?ABCD的面积为8,则△DEF的面积为3,其中正确结论的序号是②③④(把所有正确结论的序号填在横线上)
如图,在?ABCD中,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为点E、F,有下列结论:①AB=2DF;②DE•CF=DF•AE;③∠DFE=∠CDB;④如果?ABCD的面积为8,则△DEF的面积为3,其中正确结论的序号是②③④(把所有正确结论的序号填在横线上) 分析 根据平行四边形的对角相等可得∠C=∠A=60°,对边相等可得CD=AB,然后解直角三角形可得DF=$\frac{\sqrt{3}}{2}$CD,再求出①错误;根据两角对应相等,两三角形相似求出△ADE和△CDF相似,根据相似三角形对应边成比例求出②正确;再求出∠EDF=60°,然后根据两边对应成比例,夹角相等求出△ABD和△DFE相似,根据相似三角形对应角相等可得∠DFE=∠ABD,再根据两直线平行,内错角相等可得∠CDB=∠ABD,然后求出③正确;根据平行四边形的对角线把平行四边形分成两个面积相等的三角形求出△ABD的面积,再根据相似三角形面积的比等于相似比的平方求解即可得到△DEF的面积为3,从而判断出④正确.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,∠C=∠A=60°,
∵DF⊥BC,
∴DF=$\frac{\sqrt{3}}{2}$CD,
∴$\sqrt{3}$CD=2DF,
∴$\sqrt{3}$AB=2DF,故①错误;
∵∠A=∠C=60°,
∠AED=∠CFD=90°,
∴△ADE∽△CDF,
∴$\frac{DE}{DF}$=$\frac{AE}{CF}$,
∴DE•CF=DF•AE,故②正确;
∵∠A=∠C=60°,DE⊥AB,DF⊥BC,
∴∠ADE=∠CDF=90°-60°=30°,
∵∠A=60°,AB∥CD,
∴∠ADC=180°-60°=120°,
∴∠EDF=120°-60°=60°,
∴∠A=∠EDF=60°,
∵$\frac{DE}{DF}$=$\frac{AE}{CF}$=$\frac{AD}{CD}$=$\frac{AD}{AB}$,
∴△ABD∽△DFE,
∴∠DFE=∠ABD,
∵AB∥CD,
∴∠CDB=∠ABD,
∴∠CDB=∠DFE,故③正确;
∵?ABCD的面积为8,
∴△ABD的面积为4,
设△DEF的面积为S,
则$\frac{S}{4}$=($\frac{DE}{AD}$)2=($\frac{\sqrt{3}}{2}$)2=$\frac{3}{4}$,
所以,S=3,
即△DEF的面积为3,故④正确.
综上所述,结论正确的是②③④.
故答案为:②③④.
点评 本题考查了平行四边形的性质,相似三角形的判定与性质,三角形的面积,平行线的性质,难点在于③求出△ABD和△DFE相似,再根据相似三角形对应角相等求解.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种板材(m2/套) | 乙种板材(m2/套) | 获利(元/套) | |
| A款 | 3 | 7 | 600 |
| B款 | 5 | 3 | 400 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
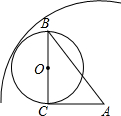 如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=3cm,⊙O是以BC为直径的圆,如果⊙O与⊙S相内切,那么⊙A的半径为$\sqrt{13}+2$cm.
如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=3cm,⊙O是以BC为直径的圆,如果⊙O与⊙S相内切,那么⊙A的半径为$\sqrt{13}+2$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com