
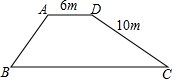
 如图是一座堤坝的横断面,AB坡坡角为45°,DC坡坡度为1:2,其他数据如图所示,求BC的长(精确到0.1m).(参考数据:$\sqrt{2}$≈1.414,$\sqrt{5}$≈2.236)
如图是一座堤坝的横断面,AB坡坡角为45°,DC坡坡度为1:2,其他数据如图所示,求BC的长(精确到0.1m).(参考数据:$\sqrt{2}$≈1.414,$\sqrt{5}$≈2.236) 分析 根据题意可以作辅助线AE⊥BC,作DF⊥BC,然后根据AB坡坡角为45°,DC坡坡度为1:2和题目中的数据可以分别求得CF和BE的长,从而可以求得BC的长.
解答 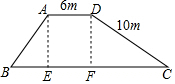 解:作AE⊥BC于点E,作DF⊥BC于点F,如右图所示,
解:作AE⊥BC于点E,作DF⊥BC于点F,如右图所示,
由题意可得,
tan∠C=$\frac{DF}{CF}=\frac{1}{2}$,CD=10m,∠B=45°,AD=6m,
∵AE⊥BC,DF⊥BC,
∴∠AEB=∠DFC=90°,AE=DF,
设DF=x,则CF=2x,
∴$\sqrt{{x}^{2}+(2x)^{2}}=1{0}^{2}$,
解得,x=2$\sqrt{5}$,
∴DF=2$\sqrt{5}$m,CF=4$\sqrt{5}$m,AE=2$\sqrt{5}$m,
∵∠AEB=90°,∠ABE=45°,AE=2$\sqrt{5}$m,
∴BE=2$\sqrt{5}$m,
∴BC=BE+EF+CF=$2\sqrt{5}+6+4\sqrt{5}$=$6\sqrt{5}+6$≈6×2.236+6=19.416≈19.4m,
即BC的长是19.4m.
点评 本题考查解直角三角形的应用-坡度坡角问题,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用勾股定理和直角三角形的性质解答.


科目:初中数学 来源: 题型:解答题
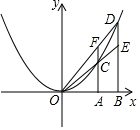 如图,在x轴上有两点A(m,0),B(n,0)(n>m>0),分别过点A,点B作x轴的垂线,交抛物线y=x2于点C,点D.直线OC交直线BD于点E,直线OD交直线AC于点F,点E,点F的纵坐标分别记作yE,yF
如图,在x轴上有两点A(m,0),B(n,0)(n>m>0),分别过点A,点B作x轴的垂线,交抛物线y=x2于点C,点D.直线OC交直线BD于点E,直线OD交直线AC于点F,点E,点F的纵坐标分别记作yE,yF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在扇形OACB中,∠AOB=120°,⊙O′为弓形ACB的最大的内切圆,若AB的长为2π,则⊙O′的周长为( )
在扇形OACB中,∠AOB=120°,⊙O′为弓形ACB的最大的内切圆,若AB的长为2π,则⊙O′的周长为( )| A. | π | B. | $\frac{2}{3}$π | C. | $\frac{3}{2}$π | D. | 2π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com