
【题目】毕达哥拉斯学派对“数”与“形”的巧妙结合作了如下研究: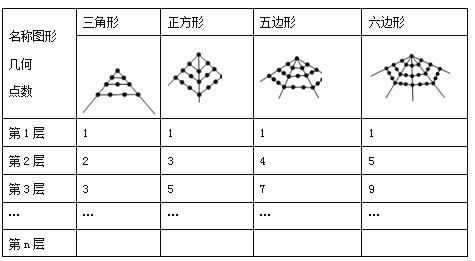
(1)六边形第5层的几何点数是 ;第n层的几何点数是 .
(2)在第 层时,六边形的几何点数是三角形的几何点数的3.5倍.
【答案】17;4n-3;6
【解析】解:(1)∵六边形第1层几何点数:1=4×1﹣3;
六边形第2层几何点数:5=4×2﹣3;
六边形第3层几何点数:9=4×3﹣3;
∴六边形第5层几何点数为:4×5﹣3=17,
六边形第n层几何点数为:4n﹣3;
(2)∵三角形第一层点数为1,第二层点数为2,第三层点数为3,
∴三角形第n层的几何点数为n;
由六边形的几何点数是三角形的几何点数的3.5倍,得
4n﹣3=3.5n,解得n=6;
则在第6层时,六边形的几何点数是三角形的几何点数的3.5倍.
所以答案是:(1)17,4n﹣3;(2)6.
【考点精析】认真审题,首先需要了解解一元一次方程的步骤(先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了).


科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中, ![]() 点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且
点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且![]() .
.
(1)判断![]() 与
与![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(2)若BE=12,CF=5,求△![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD(四边相等,四个角都是直角)的边长为4,点P从点A出发,以每秒1个单位长度的速度沿射线AD向点D运动;点Q从点D同时出发,以相同的速度沿射线AD方向向右运动,当点P到达点D时,点Q也停止运动,连接BP,过点P作BP的垂线交过点Q平行于CD的直线l于点E,BE于CD相交于点F,连接PF,设点P运动时间为t(s),
(1)求∠PBE的度数;
(2)当t为何值时,△PQF是以PF为腰的等腰三角形?
(3)试探索在运动过程中△PDF的周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,∠BOC=30°,射线OM平分∠AOC,ON平分∠BOC. 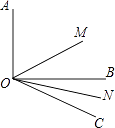
(1)求∠MON的度数;
(2)如果(1)中,∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中,∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)、(2)、(3)的结果中,你能看出什么规律?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com