
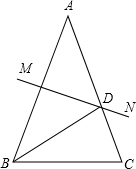
 如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC=30度.
如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC=30度. 分析 根据等腰三角形两底角相等求出∠ABC的度数,再根据线段垂直平分线上的点到线段两端点的距离相可得AD=BD,根据等边对等角的性质可得∠ABD=∠A,然后求解即可.
解答 解:∵AB=AC,∠A=40°,
∴∠ABC=$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$×(180°-40°)=70°,
∵MN垂直平分线AB,
∴AD=BD,
∴∠ABD=∠A=40°,
∴∠DBC=∠ABC-∠ABD=70°-40°=30°.
故答案为:30.
点评 本题主要考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等腰三角形两底角相等的性质,等边对等角的性质,是基础题,熟记性质是解题的关键.


科目:初中数学 来源: 题型:填空题
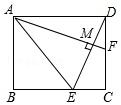 如图所示,在矩形ABCD中,F是DC上一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MF的长是$\frac{\sqrt{15}}{15}$.
如图所示,在矩形ABCD中,F是DC上一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MF的长是$\frac{\sqrt{15}}{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
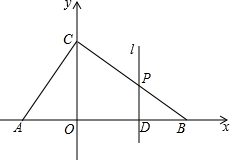 如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,点C在y轴上,∠ACB=90°,OC、OB的长分别是一元二次方程x2-6x+8=0的两个根,且OC<OB.
如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,点C在y轴上,∠ACB=90°,OC、OB的长分别是一元二次方程x2-6x+8=0的两个根,且OC<OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
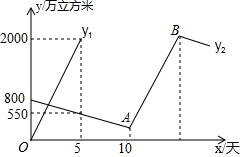 因南方旱情严重,乙水库的蓄水量以每天相同的速度持续减少,为缓解旱情,北方甲水库立即以管道运输的方式给予支援,如图是乙水库的蓄水量y1(单位:万立方米)关于时间x(单位:天)的函数图象和甲水库输水量y1(单位:万立方米)关于时间x(0≤x≤5)的函数图象,在单位时间内、甲水库的放水量与乙水库的进水量相同(水在排放、接收以及输送过程中的损耗不计),通过分析图象解答下列问题:
因南方旱情严重,乙水库的蓄水量以每天相同的速度持续减少,为缓解旱情,北方甲水库立即以管道运输的方式给予支援,如图是乙水库的蓄水量y1(单位:万立方米)关于时间x(单位:天)的函数图象和甲水库输水量y1(单位:万立方米)关于时间x(0≤x≤5)的函数图象,在单位时间内、甲水库的放水量与乙水库的进水量相同(水在排放、接收以及输送过程中的损耗不计),通过分析图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
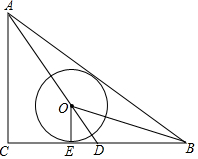 如图,△ABC中,∠C=90°,AC=3,AB=5,点O在BC边的中线AD上,⊙O与BC相切于点E,且∠OBA=∠OBC.
如图,△ABC中,∠C=90°,AC=3,AB=5,点O在BC边的中线AD上,⊙O与BC相切于点E,且∠OBA=∠OBC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则四边形AECF的周长为( )
如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则四边形AECF的周长为( )| A. | 12 cm | B. | 16 cm | C. | 20 cm | D. | 24 cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com