Question

8．如图（1），顶点为（1，-4）的抛物线与y轴交于点C（0，-3），与x轴交于A、B两点（点A在点B的右边），⊙M过A、B、C三点，交y轴于另一点D；
（1）求这条抛物线的解析式；
（2）求点M的坐标；
（3）如图（2）：连接AM、DM，将∠AMD绕点M逆时针旋转，两边MA、MD与x轴、y轴分别交于点E、F，连结EF，设AE=t，当点F落在线段OC上时，直接写出：①t的取值范围；②△EMF的面积S关于t的函数关系式．

Answer 1

分析 （1）根据顶点式设抛物线为y=a（x-1）²-4，把点C（0，-3）代入即可．
（2）设M（1，m），作MH⊥OC存在为H，对称轴与OA交于点G，因为MH=1、BG=2根据BM=CM得BG²+MG²=CH²+HM²由此列出方程求解．
（3）先证明∠DMA=90°，当点F与点O重合时求出AE=1，当点F与点C重合时求出AE=4即可知道t的范围，再证明△EFM是等腰直角三角形，求出EM利用三角形面积公式即可．

解答 解：（1）设抛物线为y=a（x-1）²-4，把点C（0，-3）代入得到a=1，
所以抛物线y=x²-2x-3，
（2）如图1，由题意A（3，0），B（-1，0），C（0，-3），

∵抛物线对称轴x=1，∴圆心M在直线x=1上，
∴设M（1，m），作MH⊥OC存在为H，对称轴与OA交于点G，
∴MH=1．，BG=2，
∵BM=CM，
∴BG²+MG²=CH²+HM²，
∴4+m²=（m+3）²+1，
∴m=-1，
∴点M坐标为（1，-1）．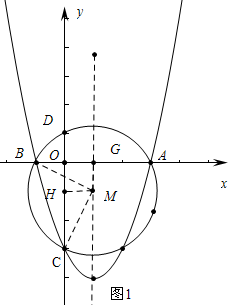

（3）如图2中，作MH⊥OC，MG⊥OA，垂足分别为H，G，
在△MDH和△MAG中，
$\left\{\begin{array}{l}{DH=AG}\\{∠MHD=∠MGA}\\{MH=MG}\end{array}\right.$，
∴△MDH≌△MAG，
∴∠HMD=∠GMA，
∴∠HMG=∠AMD=90°，
当点F与O重合时，易知∠MOE=∠MEO=45°，OG=GE=1，AE=1，
此时t=1．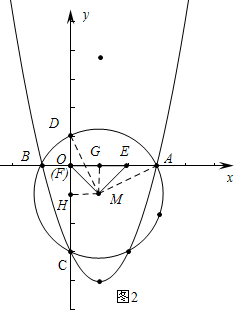

如图3中，当点F与点C重合时，
∵∠EMF=∠HMG=90°，
∴∠HMF=∠EMG，
在△MHF和△MGE中，
$\left\{\begin{array}{l}{∠HMF=∠EMG}\\{HM=MG}\\{∠MHF=∠MGE=90°}\end{array}\right.$，
∴△MHF≌△MGE，
∴EG=HF=2，此时t=4，
∴当点F落在线段OC上时，1≤t≤4．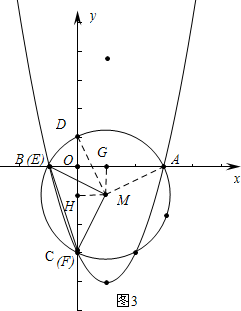

（4）1≤t≤4时，如图4中，
∵∠HMG=∠EMF=90°，
∴∠EMG=∠FMH，
在△MHF和△MGE中，
$\left\{\begin{array}{l}{∠MHF=∠MGE=90°}\\{MH=MG}\\{∠FMH=∠EMG}\end{array}\right.$，
∴△MHF≌△MGE，
，∴MF=ME=$\sqrt{M{G}^{2}+G{E}^{2}}$=$\sqrt{1+（2-{t）}^{2}}$，
∴s=$\frac{1}{2}$ME²=$\frac{1}{2}$（t²-4t+5）=$\frac{1}{2}$t²-2t+$\frac{5}{2}$．

点评 本题考查二次函数的图象与性质、垂径定理、勾股定理、等腰三角形性质、全等三角形的判定和性质、旋转等知识，注意转化的思想以及分类讨论的方法．