
【题目】如图所示,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4 , 给出如下结论:①S1+S4=S2+S3;②S2+S4=S1+S2;③若S3=2S1 , 则S4=2S2;④若S1=S2 , 则S3=S4 , 其中正确结论的序号是 . 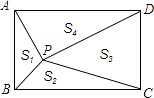
【答案】②④
【解析】解:如图,过点P分别作PF⊥AD于点F,PE⊥AB于点E, ∵△APD以AD为底边,△PBC以BC为底边,
∴此时两三角形的高的和为AB,即可得出S1+S3= ![]() 矩形ABCD面积;
矩形ABCD面积;
同理可得出S2+S4= ![]() 矩形ABCD面积;
矩形ABCD面积;
∴②S2+S4=S1+S3正确;
当点P在矩形的两条对角线的交点时,S1+S2=S3+S4 .
但P是矩形ABCD内的任意一点,所以该等式不一定成立.
故①不一定正确;
③若S3=2S1 , 只能得出△APD与△PBC高度之比,S4不一定等于2S2;
故此选项错误;
∵S2+S4=S1+S3;若S1=S2 , 则S3=S4 ,
∴④正确.
所以答案是:②④.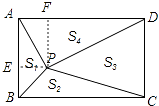
【考点精析】通过灵活运用矩形的性质,掌握矩形的四个角都是直角,矩形的对角线相等即可以解答此题.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是边BC所在的直线上的动点(点D不与B、C重合),过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.
(1)求证:AF=DE;
(2)若AC=5,DE=6,则DF= .
(3)试探究:D在不同位置时,DE,DF,AC具有怎样的数量关系,直接写出结论:
①当点D在线段BC上时,关系是:;
②当点D在线段BC延长线上时,关系是:;
③当点D在线段CB延长线上时,关系是:;
(4)请选择(3)中你探究获得的其中一个结论证明之.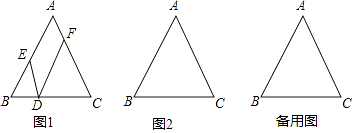
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,△ABC的三个顶点及D、E、F、G、H、五个点分别位于小正方形的顶点上. 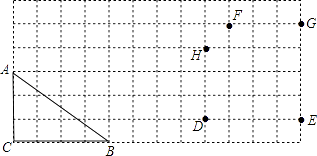
(1)画出△ABC绕点B顺时针方向旋转90°后的图形.
(2)先从E、F、G、H四个点中任意取两个不同的点,再和D点构成三角形,求所得三角形与△ABC面积相等的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算与化简:
(1)(﹣ ![]() )×(﹣12)
)×(﹣12)
(2)(﹣3)2÷(2 ![]() )﹣4×(﹣
)﹣4×(﹣ ![]() )2
)2
(3)x2y﹣3×( ![]() xy2﹣
xy2﹣ ![]() yx2)+y2x,其中x=﹣2,y=1.
yx2)+y2x,其中x=﹣2,y=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校“阅读工程”的开展情况.市教育局从该校初中生中随机抽取了150名学生进行了阅读情况的问卷调查,绘制了如下不完全的统计图: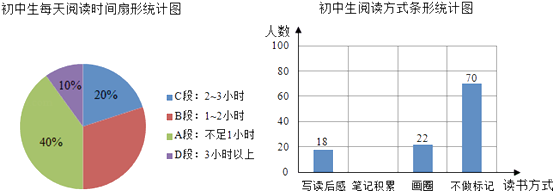
根据上述统计图提供的信息,解答下列问题:
(1)每天阅读时间在1﹣2小时学生有多少人?
(2)采用“笔记积累”阅读方式的学生有多少人?
(3)补全条形统计图.
(4)若将写读后感、笔记积累、画圈点读三种方式称为记忆阅读,求笔记积累人数占有记忆阅读人数的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2014年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2016年底三年共累计投资9.5亿元人民币建设廉租房.若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2016年底共建设了多少万平方米的廉租房?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com