
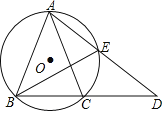
【题目】如图,△ABC内接于圆O,且AB=AC,延长BC到点D,使CD=CA,连接AD交圆O于点E.
(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为 时,四边形AOCE是菱形.
②若AE=![]() ,AB=2
,AB=2![]() ,则DE的长为 .
,则DE的长为 .
【答案】(1)详见解析;(2)①60°;②![]() .
.
【解析】
(1)根据AAS证明两三角形全等;
(2)①先证明∠AOC=∠AEC=120°,∠OAE=∠OCE=60°,可得AOCE,由OA=OC可得结论;
②由△ABE≌△CDE知AE=CE=![]() ,AB=CD=2
,AB=CD=2![]() ,,证△DCE∽△DAB得
,,证△DCE∽△DAB得![]() ,据此求解即可.
,据此求解即可.
(1)∵AB=AC,CD=CA,
∴∠ABC=∠ACB,AB=CD,
∵四边形ABCE是圆内接四边形,
∴∠ECD=∠BAE,∠CED=∠ABC,
∵∠ABC=∠ACB=∠AEB,
∴∠CED=∠AEB,
∴△ABE≌△CDE(AAS);
(2)①当∠ABC的度数为60°时,四边形AOCE是菱形;
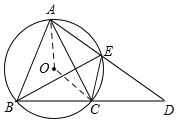
理由是:连接AO、OC,
∵四边形ABCE是圆内接四边形,
∴∠ABC+∠AEC=180°,
∵∠ABC=60,
∴∠AEC=120°=∠AOC,
∵OA=OC,
∴∠OAC=∠OCA=30°,
∵AB=AC,
∴△ABC是等边三角形,
∴∠ACB=60°,
∵∠ACB=∠CAD+∠D,
∵AC=CD,
∴∠CAD=∠D=30°,
∴∠ACD=120°,
∵∠ECD=∠BAE=60°+30°=90°,
∴∠ACE=,120°﹣90°=30°,
∴∠OAE=∠OCE=60°,
∴四边形AOCE是平行四边形,
∵OA=OC,
∴AOCE是菱形;
②∵△ABE≌△CDE,
∴AE=CE=![]() ,AB=CD=2
,AB=CD=2![]() ,
,
∵∠DCE=∠DAB,∠D=∠D,
∴△DCE∽△DAB,
∴![]() ,即
,即![]() ,
,
解得DE=![]() ,
,
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
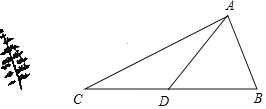
【题目】某校一棵大树发生一定的倾斜,该树与地面的夹角∠ABC=75°.小明测得某时大树的影子顶端在地面C处,此时光线与地面的夹角∠ACB=30°;又过了一段时间,测得大树的影子顶端在地面D处,此时光线与地面的夹角∠ADB=50°.若CD=8米,求该树倾斜前的高度(即AB的长度).(结果保留一位小数.参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
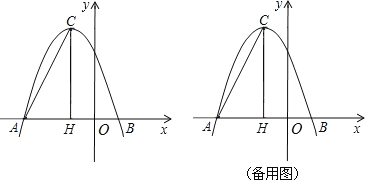
【题目】在平面直角坐标系中,抛物线y=ax2+bx+3与x轴的两个交点分别为A、B(1,0),与y轴交于点D,直线AD:![]() ,抛物线顶点为C,作CH⊥x轴于点H.
,抛物线顶点为C,作CH⊥x轴于点H.
(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使得S△ACD=![]() S△MAB?若存在,求出点M的坐标;若不存在,说明理由;
S△MAB?若存在,求出点M的坐标;若不存在,说明理由;
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,且α+β=120°,连接AD,求∠ADB的度数.(不必解答)
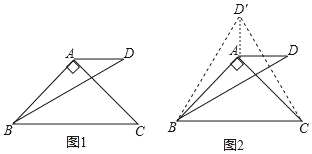
(1)小聪先从特殊问题开始研究,当α=90°,β=30°时,利用轴对称知识,以AB为对称轴构造△ABD的轴对称图形△ABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形等相关知识便可解决这个问题.
请结合小聪研究问题的过程和思路,在这种特殊情况下填空:△D′BC的形状是 三角形;∠ADB的度数为 .
(2)在原问题中,当∠DBC<∠ABC(如图1)时,请计算∠ADB的度数;
(3)在原问题中,过点A作直线AE⊥BD,交直线BD于E,其他条件不变若BC=7,AD=2.请直接写出线段BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
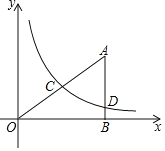
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴,垂足为点B,反比例函数y=![]() (x>0)的图象经过AO的中点C,交AB于点D,且AD=3.
(x>0)的图象经过AO的中点C,交AB于点D,且AD=3.
(1)设点A的坐标为(4,4)则点C的坐标为 ;
(2)若点D的坐标为(4,n).
①求反比例函数y=![]() 的表达式;
的表达式;
②求经过C,D两点的直线所对应的函数解析式;
(3)在(2)的条件下,设点E是线段CD上的动点(不与点C,D重合),过点E且平行y轴的直线l与反比例函数的图象交于点F,求△OEF面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
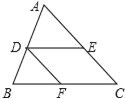
【题目】如图,在△ABC中,点D、E、F分别在边AB、AC、BC上,DE∥BC,DF∥AC,若△ADE与四边形DBCE的面积相等,则△DBF与△ADE的面积之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 3-2
D. 3-2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
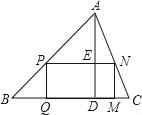
【题目】在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上,若BC=8cm,AD=6cm,且PN=2PQ,则矩形PQMN的周长为( )
A. 14.4cmB. 7.2cmC. 11.52cmD. 12.4cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com