
����Ŀ����ͼ1�����ǰѶԽ����ഹֱ���ı��ν��������ı��Σ�

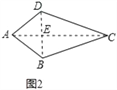
(l)�������⣺��ͼ2�����ı���ABCD�У�AB=AD��CB=CD�����ı���ABCD�Ǵ����ı�������˵�����ɣ�
(2)����̽峣���̽�������ı���ABCD����Ա�AB��CD��BC��AD֮���������ϵ��
�������:��Ҫ������������������
д��֤�����̣��Ȼ���ͼ�Σ�д����֪����֤��
(3)����������ͼ3���ֱ���Rt��ACB��ֱ�DZ�AC��б��ABΪ��������������ACFG��������ABDE������CE��BG��GE����֪AC=4��AB=5,��GE����

���𰸡���1���ı���ABCD�Ǵ����ı���,���ɼ�����;��2��������ۣ������ı��ε�����Աߵ�ƽ�������,���̼�����;��3��GE=![]()
�������������������1�����ݴ�ֱƽ���ߵ��ж������ɵã�ֱ��AC���߶�BD�Ĵ�ֱƽ���ߣ����۵�֤��
��2�����ݴ�ֱ�Ķ���ɵá�AED=��AEB=��BEC=��CED=90�����ɹ��ɶ�����AD2+BC2=AE2+DE2+BE2+CE2�������õ��𰸣�
��3������CG��BE������������GAB�ա�CAE����֪��ABG=��AEC�������õ��ı���BCGE�Ǵ����ı��Σ����������ݴ����ı��ε����ʡ����ɶ����Լ���2���Ľ��۽��м�����⣬������ɽ��.
���������
�⣺��1���ı���ABCD�Ǵ����ı��Σ�
֤������AB=AD��
���A���߶�BD�Ĵ�ֱƽ�����ϣ�
��CB=CD��
���C���߶�BD�Ĵ�ֱƽ�����ϣ�
��ֱ��AC���߶�BD�Ĵ�ֱƽ���ߣ�
��AC��BD�����ı���ABCD�Ǵ����ı��Σ�
��2��������ۣ������ı��ε�����Աߵ�ƽ������ȣ�
��ͼ2����֪�ı���ABCD�У�AC��BD������ΪE��
��֤��AD2+BC2=AB2+CD2
֤������AC��BD��
���AED=��AEB=��BEC=��CED=90����
�ɹ��ɶ����ã�AD2+BC2=AE2+DE2+BE2+CE2��
AB2+CD2=AE2+BE2+CE2+DE2��
��AD2+BC2=AB2+CD2��
��3������CG��BE��
�ߡ�CAG=��BAE=90����
���CAG+��BAC=��BAE+��BAC������GAB=��CAE��
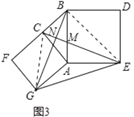
�ڡ�GAB�͡�CAE�У�
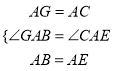 ��
��
���GAB�ա�CAE��
���ABG=��AEC���֡�AEC+��AME=90����
���ABG+��AME=90������CE��BG��
���ı���CGEB�Ǵ����ı��Σ�
�ɣ�2���ã�CG2+BE2=CB2+GE2��
��AC=4��AB=5��
��BC=3��CG=4![]() ��BE=5
��BE=5![]() ��
��
��GE2=CG2+BE2��CB2=73��
��GE=![]() ��
��


 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д� Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĸ����⣺�����������һ�ߵ��е㵽�������߾�����ȣ���ô���������һ���ǵ��������Σ��������Խ����ഹֱ����ȵ��ı����������Σ���һ������2��4��6.4�ķ�����2���ܡ�OAB���OCD����OΪλ�����ĵ�λ��ͼ�Σ���λ�Ʊ�Ϊ1��4����֪��OCD=90�㣬OC=CD����A��C�ڵ�һ���ޣ�����D����Ϊ��2 ![]() ��0�������A����Ϊ��
��0�������A������ ![]() ��
�� ![]() ����������ȷ������������ȷ�������ż��ɣ�
����������ȷ������������ȷ�������ż��ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С�ݶ���μ�ѧУ��֯����ѧ��ȤС��,����ѧУ���������,��������ֻ����1�˲μ�.��ѧ��ʦ�����һ������:��ͼ,���������ſ�Ƭ,ÿ�ſ�Ƭ�϶���һЩ��,�����������������ϱ�ʾ����,���á�<����������,˭�Ȱ���Ҫ������,˭�Ͳμ���ȤС��,��Ҳһ������һ��!
-(-2)��(-1)3��-|-3|��0���෴��
�١������ڡ��������ۡ���������
-0.4�ĵ���������-1��2.5����
�ݡ�����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʮ��һ���ƽ����ڼ䣬����ij������������7�������ÿ�����ε������仯���±���
��������ʾ��ǰһ����������������ʾ��ǰһ���ٵ�������������λ�����ˣ�
�� �� | 1�� | 2�� | 3�� | 4�� | 5�� | 6�� | 7�� |
�����仯 | + 1.2 | + 1.2 | + 0.4 | �C 0.2 | �C 0.8 | + 0.2 | �C 1.4 |
��9��30�յ�����������Ϊ3���ˣ���
��1�������10��5�յ�����������
��2�����ж�7��������������������һ�죿���ٵ�����һ�죿�������������ˣ�
��3�����þ�����ƱΪÿ��20Ԫ��������þ���ƽ����ڼ�����빲������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����µ�ʽ��
![]()
![]()
![]()
![]()
��
![]() �����������
�����������![]() ________
________
![]() ֱ��д�������
ֱ��д�������![]() ________
________
![]() ���㣺
���㣺![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O��ֱ����C�ǡ�O��һ�㣬��BAC��ƽ���߽���O�ڵ�D������O������BE�ڵ�E������D��DF��AC����AC���ӳ����ڵ�F�� 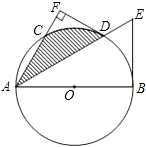
��1����֤��DF�ǡ�O�����ߣ�
��2����DF=3��DE=2 ���� ![]() ֵ��
ֵ��
����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��cΪ�����ʵ������![]() �Ŀ���ֵ�ĸ���Ϊ��������
�Ŀ���ֵ�ĸ���Ϊ��������
A. 4 B. 5 C. 6 D. 7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ׯ�ƻ�����A��B�����ͺŵ������ع�20�����Խ���ô�����ũ����ȼ�����⣮�����ͺ������ص�ռ������Ϳɹ�ʹ��ũ�������±���
�ͺ� | ռ����� ����λ��m2/���� | �ɹ�ʹ��ũ���� ����λ����/���� |
A | 15 | 18 |
B | 20 | 30 |
��֪�ɹ����������ص�ռ�����������365m2���ô�ũ������492����
��1����κ������佨��A��B�ͺ������������ĸ��������������������������ķ����м��֣�ͨ������ֱ�д�����ַ�����
��2����д������A��B�����ͺŵ��������������ܷ���y�ͽ���A����������������x֮��ĺ�����ϵʽ��
��3����A�ͺ�����������ÿ�����2��Ԫ��B�ͺ�����������ÿ�����3��Ԫ����˵���ڣ�1���еĸ��ֽ��췽���У����ֽ��췽����ʡǮ�����ٵķ�����Ҫ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�������Σ��Խ���AC��BD�ཻ�ڵ�O��
��1����ͼ1����P��������ABCD��һ�㣬����OP����OPΪһ�ߣ���������OPMN���ұ�ON���BC�ཻ������AP��BN��
�������ⲹȫͼ1��
���ж�AP��BN��������ϵ��λ�ù�ϵ��д�����۲�����֤����
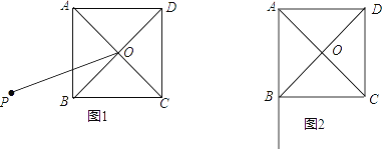
��2����P��AB�ӳ����ϣ�����APO=30��������OP����OPΪһ�ߣ���������OPMN���ұ�ON��BC���ӳ���ǡ���ڵ�N������CM����AB=2����CM�ij�������д����������������CM���Ĺ��̣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com