
 如图,取一张长方形纸片ABCD,沿AD边上任意一点M折叠后,点D、C分别落在D′、C′的位置,设折痕为MN,D′C′交BC于点E且∠AMD′=α,∠NEC′=β
如图,取一张长方形纸片ABCD,沿AD边上任意一点M折叠后,点D、C分别落在D′、C′的位置,设折痕为MN,D′C′交BC于点E且∠AMD′=α,∠NEC′=β分析 (1)α+β=90°.如图1,延长MD′交BC于点F.利用平行线的性质得到:∠AM D′=∠MFE=α.然后根据折叠的性质推知:∠MFE+∠D′EF=90°,∠D′EF=∠NEC′,故α+β=90°;
(2)当点D′与点B重合时,△AD′M与△C′EN全等.如图2,此时,B、E、D′三点重合.利用折叠的性质和全等三角形的判定定理HL证得这两个三角形全等;
解答 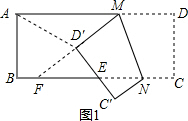 解:(1)α+β=90°.理由如下:
解:(1)α+β=90°.理由如下:
如图1,延长MD′交BC于点F.
∵AD∥BC,
∴∠AM D′=∠MFE=α.
又∠MD′E=∠D=90°,∠FD′E=90°,
∴∠MFE+∠D′EF=90°,∠D′EF=∠NEC′,
故α+β=90°;
(2)当点D′与点B重合时,△AD′M与△C′EN全等.
如图2,此时,B、E、D′三点重合.
∵由折叠可知,∠1=∠2,
∴∠C′=∠C=∠A=90°,C′E=CD.
∵AD∥BC,∠2=∠3,
得∠1=∠3,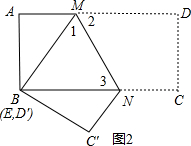
即D′M=EN.
又AD′=DC,
∴AD′=C′E,
∴在Rt△AD′M与Rt△C′EN中,
$\left\{\begin{array}{l}{AD′=CE′}\\{D′M=EN}\end{array}\right.$,
故Rt△AD′M≌Rt△C′EN(HL).
点评 本题综合考查了矩形的性质、折叠的性质、等腰三角形的判定与性质以及全等三角形的判定与性质等知识.难度比较大,需要学生对所学的知识有一个系统的掌握;另外,对于等腰三角形的顶点不确定的问题,需要分类讨论,以防漏解.


科目:初中数学 来源: 题型:选择题
| A. | 检测某城市的空气质量 | B. | 调查全国初中生的视力情况 | ||
| C. | 审查某篇文章的错别字 | D. | 调查某池塘中现有鱼的数量 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查高邮市民的吸烟情况 | |
| B. | 调查高邮市民的幸福指数 | |
| C. | 调查高邮市民家族日常生活支出情况 | |
| D. | 调查高邮市某校班级学生对“文明城市”的知晓率 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | -2 | C. | -4 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com