
����������12�֣���ͼ������OABC�Ķ���A��C�ֱ���x��y����������ϣ���DΪ�Խ���OB���е㣬��E��4��n���ڱ�AB�ϣ�����������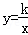 ��k��0���ڵ�һ�����ڵ�ͼ����D��E����D��ĺ������������������2����
��k��0���ڵ�һ�����ڵ�ͼ����D��E����D��ĺ������������������2����
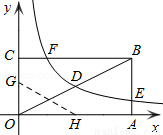
��1�����AB�ij���
��2�����������Ľ���ʽ��n��ֵ��
��3����������������ͼ������εı�BC���ڵ�F���������۵���ʹ��O���F�غϣ��ۺ۷ֱ���x��y�������ύ�ڵ�H��G�����߶�OG�ij���
��1��BA��2����2�������������Ĺ�ϵʽΪy��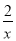 �� n��
�� n��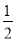 ����3��OG��
����3��OG��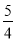 ��
��
��������
��1����E��4��n������OA��4����D�������������������2������BA��OA��1��2����BA��4��1��2����BA��2��
��2����OA��4��AB��2����B��4��2�����ߵ�DΪOB���е㣬��D��2��1�����ߵ�D�ڷ�����������ͼ���ϣ�
��1��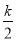 ����k��2���෴���������Ĺ�ϵʽΪy��
����k��2���෴���������Ĺ�ϵʽΪy��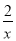 ����E��4��n���ڷ�����������ͼ���ϣ���n��
����E��4��n���ڷ�����������ͼ���ϣ���n��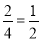 ��
��
��3����B��4��2����BC��x�ᣬ���F�����������2���ߵ�FҲ�ڷ�����������ͼ���ϣ���F��1��2������CF��1������GF����OG��GF��x����OC��2��CF2��GF2����Rt��GCF�У�CG2��CF2��GF2������2��x��2��12��x2�����x��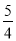 ����x��
����x��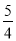 ����OG��
����OG��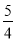 ��
��
���㣺�����������ۺ��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2015���ʱͬ����ϰ����̰棩���꼶��1.3���κ���������1�������棩 ���ͣ�?????
��ͼ��ʾ���������Ƕ��κ���y=ax2+5x+4��a2��ͼ����ôa��ֵ�ǣ� ��
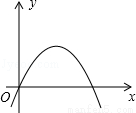
A.2 B.��2 C.��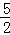 D.��2
D.��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���꼶��ѧ�ڵڶ����¿���ѧ�Ծ��������棩 ���ͣ������
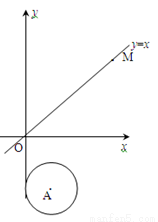
����������12�֣���ͼ����ƽ��ֱ������ϵ�У���A�İ뾶Ϊ1��Բ��A�������Ϊ��1����2����ֱ��OM��һ�κ���y=x��ͼ���á�A��y����������ÿ��1����λ�����ƶ����ƶ�ʱ��Ϊt��
��1�����
��ֱ��OM��x�����е���Ƕ���Ϊ �㣻
�ڵ�t= ʱ����A�������������������㣻
��2����t��3ʱ������˶������С�A��ֱ��OM����ʱ��t��ֵ��
��3���˶������У�����A��ֱ��OM�ཻ���õ��ҳ�Ϊ1ʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���꼶��ѧ�ڵڶ����¿���ѧ�Ծ��������棩 ���ͣ������
������x�ķ���x2��mx��2��0��������ȵ�ʵ��������m��ֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���꼶��ѧ�ڵڶ����¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
һ�������Ŀڴ�����4����״��ȫ��ͬ�Ŀ�Ƭ,�ֱ�д������1,2,3,4,�ڴ��������ſ�Ƭ,�ֱ�д������2,3,������ӿڴ���ȡ��һ�ſ�Ƭ,�����ſ�Ƭ��ڴ�������ſ�Ƭ�ϵ�����Ϊ���������ߵij�,�ܹ��������εĸ����ǣ� ��
A. B.
B. C.
C. D.1
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭������и۳�ʵ��ѧУ���꼶��ѧ�����е�����ѧ�Ծ� �������棩 ���ͣ������
����������10�֣���ͼ����ֱ������ϵxOy�У�ֱ��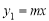 ��˫����
��˫����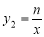 �ཻ��
�ཻ��
A����1��a����B���㣬BC��x�ᣬ����ΪC����BOC�������1��

��1����m��n��ֵ��
��2����ֱ��AC�Ľ���ʽ��
��3�����ͼ��ֱ��д����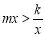 ʱ��
ʱ��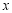 ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭������и۳�ʵ��ѧУ���꼶��ѧ�����е�����ѧ�Ծ� �������棩 ���ͣ������
����������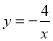 ����
����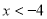 ʱ��
ʱ��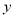 ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��ɽ��ʡ̩���������꼶��ѧ����ĩģ����ѧ�Ծ��������棩 ���ͣ������
��ͼ���ֱ���Rt��ABC��ֱ�DZ�AC��б��AB�������ȱߡ�ACD���ȱߡ�ABE����֪��BAC=30�㣬EF��AB������ΪF������DF��
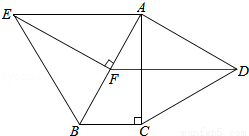
��1����˵��AC=EF��
��2����֤���ı���ADFE��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��ɽ��ʡ���꼶��ѧ�ڵ������¿���ѧ���������棩 ���ͣ�ѡ����
��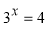 ,
, ����
����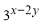 ��ֵΪ�� ��
��ֵΪ�� ��
A��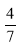 B��
B��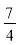 C��
C��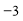 D��
D��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com