
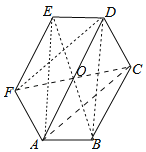
【题目】如图,六边形ABCDEF的内角都相等,∠DAB=60°,AB=DE,则下列结论成立的个数是( )
①AB∥DE;②EF∥AD∥BC;③AF=CD;④四边形ACDF是平行四边形;⑤六边形ABCDEF既是中心对称图形,又是轴对称图形.

A. 2 B. 3 C. 4 D. 5
【答案】D
【解析】试题解析:∵六边形ABCDEF的内角都相等,∴∠EFA=∠FED=∠FAB=∠ABC=120°,∵∠DAB=60°,∴∠DAF=60°,∴∠EFA+∠DAF=180°,∠DAB+∠ABC=180°,∴AD∥EF∥CB,故②正确,∴∠FED+∠EDA=180°,∴∠EDA=∠ADC=60°,∴∠EDA=∠DAB,∴AB∥DE,故①正确,∵∠FAD=∠EDA,∠CDA=∠BAD,EF∥AD∥BC,∴四边形EFAD,四边形BCDA是等腰梯形,∴AF=DE,AB=CD,∵AB=DE,∴AF=CD,故③正确,连接CF与AD交于点O,连接DF、AC、AE、DB、BE.
∵∠CDA=∠DAF,∴AF∥CD,AF=CD,∴四边形AFDC是平行四边形,故④正确,同法可证四边形AEDB是平行四边形,∴AD与CF,AD与BE互相平分,∴OF=OC,OE=OB,OA=OD,∴六边形ABCDEF既是中心对称图形,故⑤正确,故选D.


科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG. 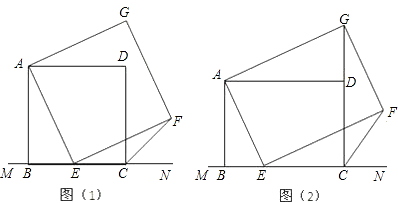
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数,并说明理由;
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
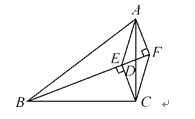
【题目】如图所示,BD是△ABC的中线,CE⊥BD于点E,AF⊥BD,交BD的延长线于点F.
(1)试探索BE,BF和BD三者之间的数量关系,并加以证明;
(2)连接AE,CF,求证:AE∥CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高铁的开通,给N市市民出行带来了极大的方便,“元旦”期间,甲、乙两人应邀到A市的艺术馆参加演出,甲乘私家车从N市出发1小时后,乙乘坐高铁从N市出发,先到A市火车站,然后再转乘出租车到A市的艺术馆(换车时间忽略不计),两人恰好同时到达A市的艺术馆,他们离开N市的距离y(千米)与乘车时间x(小时)的关系如图所示,请结合图象解答下列问题: 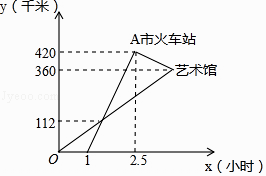
(1)高铁的平均速度是每小时多少千米?
(2)分别求甲、乙(乘坐高铁时)两人离开N市的距离y与乘车时间x的函数关系式;
(3)若甲要提前30分钟到达艺术馆,那么私家车的速度必须达到多少千米/小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】煤气公司一工人检修一条长540米的煤气管道,计划用若干小时完成,在实际检修过程中,每小时检修的管道长度是原计划的1.5倍,结果提前3小时完成任务,求该工人原计划每小时检修煤气管道多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,6),B(b,0),且b<0,点C,D分别是OA,AB的中点,△AOB的外角平分线与CD的延长线交于点E.
(1)求证:∠DAO=∠DOA;
(2)①若b=-8,求CE的长;
②若CE=![]() +1,则b=________.
+1,则b=________.
(3)是否存在这样的b值,使得四边形OBED为平行四边形?若存在,请求出此时四边形OBED对角线的交点坐标;若不存在,请说明理由.
(4)直线AE与x轴交于点F,请用含b的式子直接写出点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.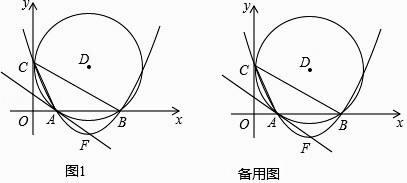
(1)D点的坐标是 , 圆的半径为;
(2)求经过C、A、B三点的抛物线所对应的函数关系式;
(3)设抛物线的顶点为F,试证明直线AF与圆D相切;
(4)在x轴下方的抛物线上,是否存在一点N,使△CBN面积最大,最大面积是多少?并求出N点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com