
【题目】已知等边△ABC中,点D,E分别在边AB, BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′,EB′分别交边AC于点F,G,若∠ADF=80°,则∠EGC的度数为( )。

A. 70°B. 75°C. 80°D. 85°
【答案】C
【解析】
根据△DEB′是△BDE沿直线DE翻折得到的,得到∠B=∠B′,根据等边三角形的性质可得∠A=∠C=∠B=60°,根据三角形内角和定理可求得∠AFD=40°,继而可求得∠∠B′GF=80°,再根据对顶角的性质即可求得答案.
∵△DEB′是△BDE沿直线DE翻折得到的,
∴∠B=∠B′,
∵△ABC是等边三角形,
∴∠A=∠C=∠B=60°,
∵∠A+∠ADF+∠AFD=180°,∠ADF=80°,
∴∠AFD=180°-60°-80°=40°,
∵∠B′FG+∠B′GF+∠B′=180°,∠B′FG=∠AFD,
∴∠B′GF=180°-60°-40°=80°,
∴∠EGC=∠B′GF=80°,
故选C.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只![]() 型节能灯和3只
型节能灯和3只![]() 型节能灯共需11元;3只
型节能灯共需11元;3只![]() 型节能灯和2只
型节能灯和2只![]() 型节能灯共需12元.
型节能灯共需12元.
(1)求一只![]() 型节能灯和一只
型节能灯和一只![]() 型节能灯的售价各是多少元?
型节能灯的售价各是多少元?
(2)学校准备购进这两种型号的节能灯共30只,并且![]() 型节能灯的数量不多于
型节能灯的数量不多于![]() 型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEC中,AB=DE.若添加条件后使得△ABC≌△DEC,则在下列条件中,不能添加的是( )

A. BC=EC,∠B=∠E B. BC=EC,AC=DC
C. ∠B=∠E,∠A=∠D D. BC=EC,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
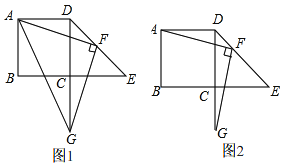
【题目】在正方形![]() 中,点
中,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,点
,点![]() 为
为![]() 边上一点,连接
边上一点,连接![]() ,作
,作![]() 交直线
交直线![]() 于点
于点![]() .
.
(1)如图1,填空:![]() _____________;
_____________;
(2)如图1,连接![]() ,若
,若![]() ,求
,求![]() 的面积;
的面积;
(3)如图2,若![]() 时,求证:DG=
时,求证:DG=![]() +AD.
+AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年春节,一场新冠病毒疫情由武汉开始席卷了整个中华地区,全国人民齐心协力、共同抗疫.为了防止感染,![]() 口罩成为了大众纷纷抢购的必需品,由于需求增加导致价格不断走高,引起了民众与政府的高度关注,据统计:2020年2月份一盒
口罩成为了大众纷纷抢购的必需品,由于需求增加导致价格不断走高,引起了民众与政府的高度关注,据统计:2020年2月份一盒![]() 口罩价格比2020年1月份上涨了
口罩价格比2020年1月份上涨了![]() ,某市民2020年2月3日在某超市订购了一盒
,某市民2020年2月3日在某超市订购了一盒![]() 口罩花了52元.
口罩花了52元.
(1)问:2020年1月份一盒![]() 口罩的价格为多少元?
口罩的价格为多少元?
(2)某超市将进货价为每盒39元的![]() 口罩,按2020年2月3日价格出售,平均一天能销售出100盒,经调查表明:
口罩,按2020年2月3日价格出售,平均一天能销售出100盒,经调查表明:![]() 口罩的售价每盒下降1元,其口罩销售量就增加10盒,超市为了实现销售
口罩的售价每盒下降1元,其口罩销售量就增加10盒,超市为了实现销售![]() 口罩每天有1320元的利润,并且尽可能让顾客得到实惠,每盒
口罩每天有1320元的利润,并且尽可能让顾客得到实惠,每盒![]() 口罩的售价应该下降多少元?
口罩的售价应该下降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
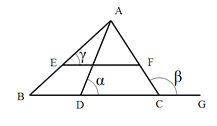
【题目】如图,在△ABC中,EF∥BC,∠ACG是△ABC的外角,∠BAC=3∠BAD,记∠ADC=![]() ,∠ACG=
,∠ACG=![]() ,∠AEF=
,∠AEF=![]() ,则:(1)
,则:(1)![]() __
__![]() (填“>”、“=”或“<”号);
(填“>”、“=”或“<”号);
(2)![]() 、
、![]() 、
、![]() 三者间的数量关系式是_______________.
三者间的数量关系式是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BE、BF分别是∠ABC与它的邻补角∠ABD的平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F,EF分别交边AB、AC于点M和N.求证:
(1)四边形AFBE是矩形;
(2)MN=![]() BC.
BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上午8时,一条船从海岛A出发,以15海里/时的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得∠BAC=60°,点C在点B的正西方向,海岛B与灯塔C之间的距离是_____海里.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
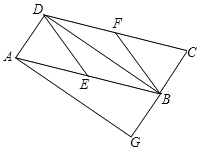
(1)求证:△ADE≌△CBF;
(2)若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com