
分析 (1)①先作出CD的垂直平分线,即可作出图形;
②先判断出△ABC是直角三角形,即可得出,EF是⊙O的直径,再用平行线的性质和同弧所对的圆周角相等得出∠A=∠CDF,进而得出∠CFD=90°,得出判断出CD是直径即可;
③利用圆中直径大于等于圆中任何一条弦即可得出CD是直径时,EF最小;
(2)先得出CD⊥AB时,CD最小,即:EF最小,最后用面积公式即可求出.
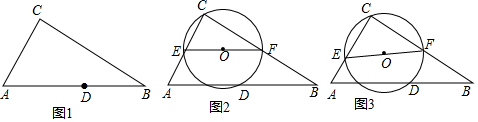
解答 解:(1)
①如图1,所示 ,
,
②如图2,连结CD,FD,
∵AC=6,BC=8,AB=10,
∴AC2+BC2=AB2
∴△ABC是直角三角形,∠ACB=90°,
∴EF是⊙O的直径,
∵D是AB中点,
∴DA=DB=DC=5,
∴∠B=∠DCB,
∵EF∥AB,
∴∠A=∠CEF,
∵∠CDF=∠CEF,
∴∠A=∠CDF,
∵∠A+∠B=90°,
∴∠CDF+∠DCB=90°,
∴∠CFD=90°,
∴CD是⊙O的直径,
∴EF=CD=5,
③
由AC2+BC2=AB2可得∠ACB=90°,
所以,EF是⊙O的直径.
由于CD是⊙O的弦,
所以,有EF≥CD,
所以,当CD是⊙O的直径时,EF最小,
(2)如图3, 由(1)③知,CD是⊙O的直径时,EF最小,即:最小值为CD
由(1)③知,CD是⊙O的直径时,EF最小,即:最小值为CD
当点D在边AB上运动时,只有CD⊥AB时,CD最小,
由(1)②知,△ABC是直角三角形,
∴S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD,
∴AC•BC=AB•CD,
∴CD=$\frac{AC•BC}{AB}$=$\frac{6×8}{10}$=$\frac{24}{5}$,
故答案为:$\frac{24}{5}$.
点评 此题是圆的综合题,主要考查了基本作图,直角三角形的判定,圆的性质,三角形的面积公式,判断出CD是直径是EF最小,是解本题的关键,是一道中等难度的中考常考题.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{32}$ | B. | 1-$\frac{1}{32}$ | C. | $\frac{1}{16}$ | D. | 1-$\frac{1}{16}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )
如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )| A. | 120° | B. | 140° | C. | 150° | D. | 160° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB=2,BC=1.动点P从点B出发,沿路线B-C-D作匀速运动.那么△ABP的面积S与点P的运动路程x之间的函数图象大致是( )
如图,在矩形ABCD中,AB=2,BC=1.动点P从点B出发,沿路线B-C-D作匀速运动.那么△ABP的面积S与点P的运动路程x之间的函数图象大致是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
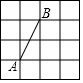 如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )
如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )| A. | 6个 | B. | 7个 | C. | 8个 | D. | 9个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com