
分析 (1)利用甲方案:月租10元,每分钟通话费0.2元;乙方案:月租0元,每分钟通话费0.3元,易得甲方案的收费为(10+0.2x)元;乙方案的收费为:0.3x元;
(2)把x=10小时=600分代入(1)中两个代数式中,计算出两代数式的值,然后通过比较代数式的值来判断选择哪种方式比较合算.
解答 解:(1)甲方案的收费为:(10+0.2x)元;
乙方案的收费为:0.3x元;
(2)当x=600时,10+0.2x=10+0.2×600=130(元);
x=600时,0.3x=0.3×600=180(元),
由于130<180,
所以择甲方案比较合算.
点评 本题考查了列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.本题的关键时根据计费方式分别表示出甲乙方案的收费.


科目:初中数学 来源: 题型:解答题
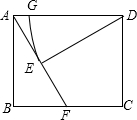 如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E
如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com